Standard deviation là gì? Đây là một khái niệm thống kê then chốt, đóng vai trò như một chiếc la bàn giúp bạn đo lường sự phân tán của một tập hợp dữ liệu so với giá trị trung bình của nó, từ đó cung cấp cái nhìn sâu sắc về tính ổn định của một tài sản tài chính.
EBC thấu hiểu rằng việc nắm bắt các công cụ phân tích phức tạp là một lợi thế cạnh tranh vượt trội. Trong bài viết này, EBC sẽ cùng bạn giải mã toàn diện về độ lệch tiêu chuẩn, biến những con số khô khan thành kiến thức hữu ích, giúp bạn tự tin hơn trên hành trình chinh phục thị trường tài chính và quản lý rủi ro hiệu quả.
Vì sao cần hiểu về độ lệnh chuẩn?
Trong thế giới tài chính đầy biến động, nơi giá cả của cổ phiếu, tiền tệ hay hàng hóa có thể thay đổi trong chớp mắt, khả năng đo lường và dự báo sự thay đổi đó không còn là một lựa chọn, mà là một yêu cầu bắt buộc để tồn tại và phát triển.
Các nhà đầu tư huyền thoại như Warren Buffett hay George Soros đều có một điểm chung: họ cực kỳ am hiểu về rủi ro. Họ không né tránh rủi ro, họ quản lý nó. Và công cụ cơ bản nhất, mạnh mẽ nhất để định lượng rủi ro chính là Độ lệch chuẩn (Standard Deviation).
Nhiều nhà giao dịch mới tham gia thị trường thường chỉ tập trung vào lợi nhuận tiềm năng mà bỏ qua thước đo về sự biến động. Họ có thể thấy một cổ phiếu tăng giá 20% trong một tháng và vội vàng đầu tư mà không nhận ra rằng cổ phiếu đó cũng có thể giảm 25% trong tháng tiếp theo.
Sự thiếu hiểu biết về mức độ phân tán của lợi nhuận chính là nguyên nhân dẫn đến những quyết định cảm tính và thua lỗ không đáng có. Standard deviation chính là lời giải cho bài toán này. Nó không chỉ cho bạn biết lợi nhuận trung bình của một khoản đầu tư là bao nhiêu, mà quan trọng hơn, nó cho bạn biết lợi nhuận đó có khả năng dao động quanh mức trung bình như thế nào.
Nắm vững khái niệm này cũng giống như việc bạn có trong tay một bản đồ thời tiết của thị trường, giúp bạn biết khi nào trời yên biển lặng và khi nào bão tố sắp ập đến.
Giải thích toàn diện Standard Deviation là gì từ A-Z
Để thực sự biến standard deviation thành một công cụ đắc lực, chúng ta cần phải đi sâu vào bản chất của nó, từ định nghĩa, ý nghĩa cho đến công thức tính toán. EBC sẽ trình bày một cách hệ thống và dễ hiểu nhất, đảm bảo rằng dù bạn là người mới bắt đầu hay đã có kinh nghiệm, bạn đều có thể nắm bắt và áp dụng.
Standard Deviation Là Gì? Định Nghĩa Từ Cơ Bản Đến Chuyên Sâu
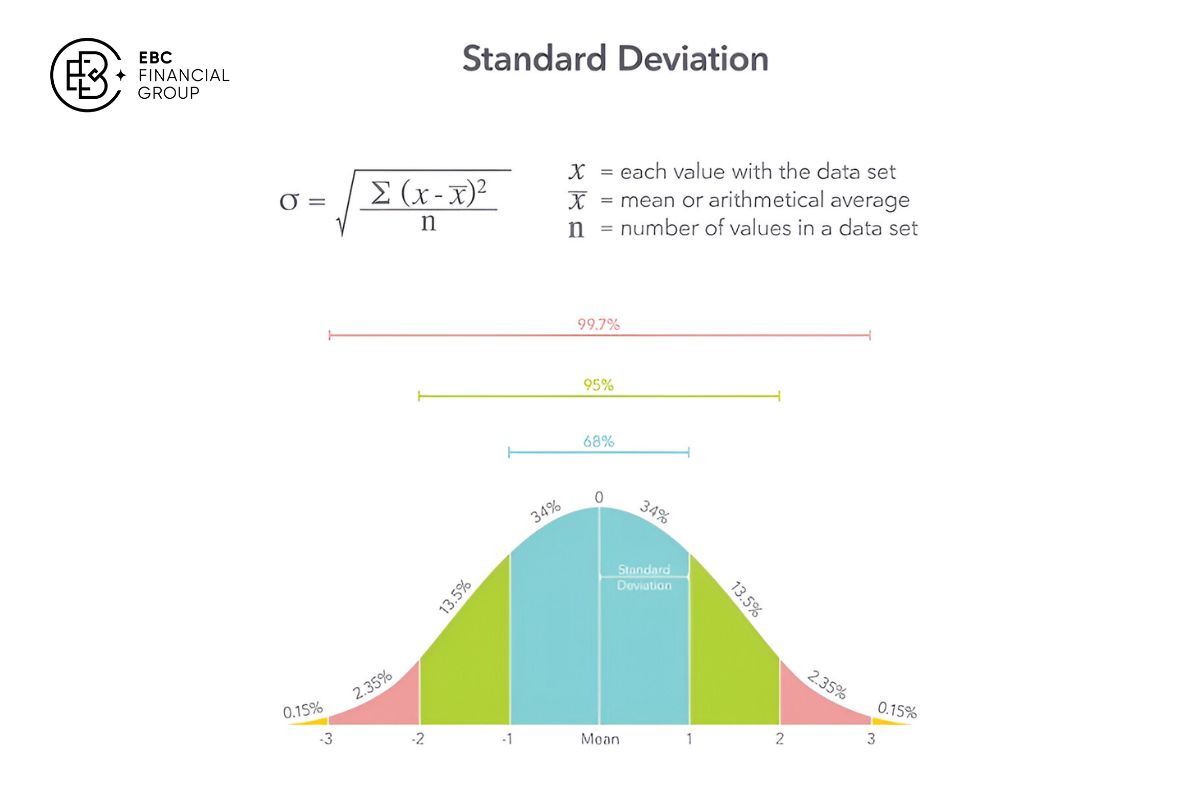
Standard deviation, hay còn gọi là độ lệch chuẩn hoặc độ lệch tiêu chuẩn, là một đại lượng thống kê mô tả dùng để đo lường mức độ phân tán hoặc lan rộng của một tập hợp dữ liệu. Cụ thể hơn, nó cho chúng ta biết các giá trị trong một chuỗi dữ liệu có xu hướng tập trung gần giá trị trung bình (mean) hay trải rộng ra xa.
Độ lệch chuẩn thấp (Low Standard Deviation): Khi giá trị độ lệch chuẩn nhỏ, điều này cho thấy các điểm dữ liệu có xu hướng tập trung rất gần với giá trị trung bình. Trong bối cảnh đầu tư, điều này ám chỉ rằng giá của tài sản ít biến động, ổn định và rủi ro thấp hơn. Ví dụ, lợi nhuận hàng tháng của một cổ phiếu blue-chip trong một ngành thiết yếu thường có độ lệch chuẩn thấp.
Độ lệch chuẩn cao (High Standard Deviation): Ngược lại, khi giá trị độ lệch chuẩn lớn, các điểm dữ liệu được phân tán trên một phạm vi rộng hơn, xa giá trị trung bình. Đối với nhà đầu tư, điều này đồng nghĩa với sự biến động giá lớn, không ổn định và mức độ rủi ro cao hơn. Các cổ phiếu công nghệ mới nổi hay tiền điện tử thường có độ lệch chuẩn rất cao, hứa hẹn lợi nhuận đột phá nhưng cũng đi kèm với nguy cơ thua lỗ lớn.
Mối quan hệ mật thiết giữa Độ lệch chuẩn và Phương sai (Variance) cần được làm rõ. Phương sai cũng là một thước đo độ phân tán, được tính bằng trung bình bình phương của các khoảng cách từ mỗi điểm dữ liệu đến giá trị trung bình. Về mặt toán học, Độ lệch chuẩn chính là căn bậc hai của Phương sai.
Việc lấy căn bậc hai giúp đưa đơn vị đo lường của độ lệch chuẩn trở về cùng đơn vị với dữ liệu gốc, giúp việc diễn giải trở nên trực quan và dễ hiểu hơn rất nhiều. Ví dụ, nếu dữ liệu của bạn là giá cổ phiếu tính bằng USD, phương sai sẽ có đơn vị là USD bình phương (USD²), một đơn vị không có ý nghĩa thực tế. Trong khi đó, độ lệch chuẩn sẽ có đơn vị là USD, cho phép bạn so sánh trực tiếp với giá cổ phiếu.
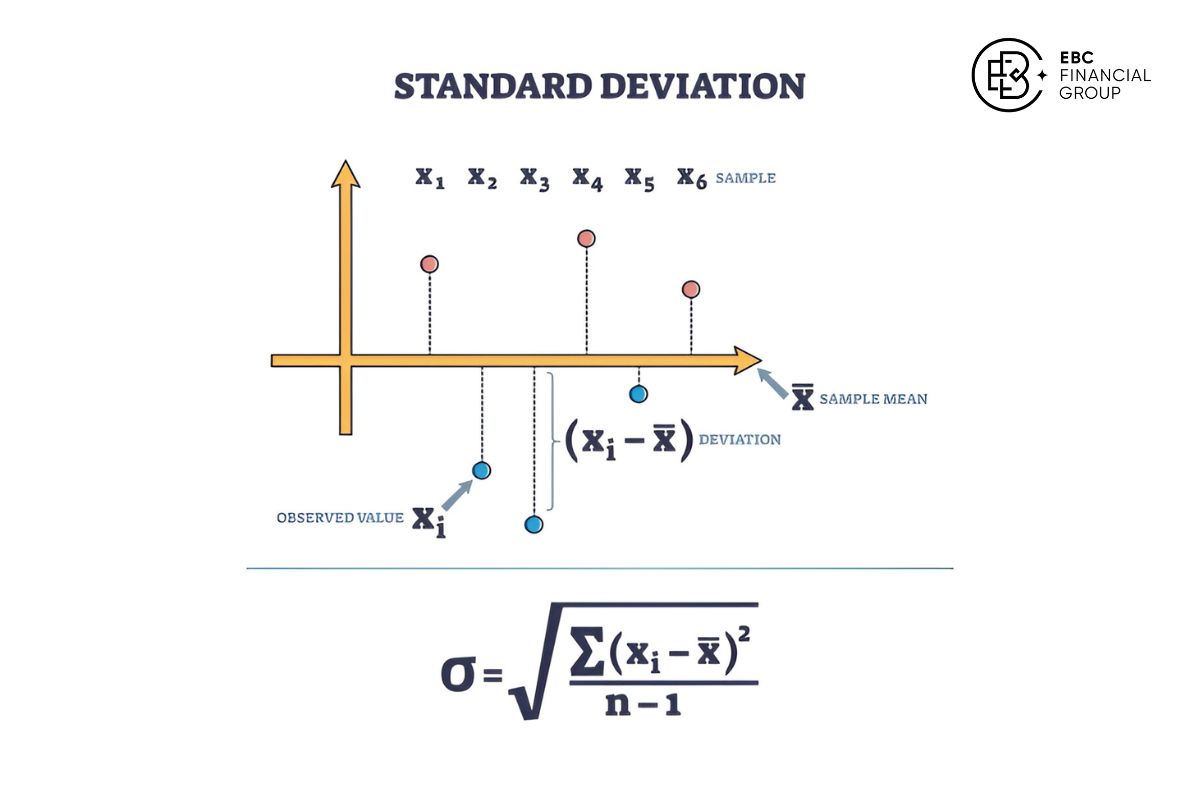
Công Thức Tính Độ Lệch Chuẩn Và Diễn Giải Từng Thành Phần
Việc hiểu công thức không chỉ giúp bạn tính toán mà còn giúp bạn thấu hiểu sâu sắc hơn về bản chất của độ lệch chuẩn. Có hai công thức chính tùy thuộc vào việc bạn đang làm việc với toàn bộ tổng thể (population) hay chỉ một mẫu (sample) từ tổng thể đó. Trong tài chính, chúng ta hầu như luôn làm việc với dữ liệu mẫu (ví dụ: giá đóng cửa trong 30 ngày qua là một mẫu của tất cả các mức giá trong lịch sử), do đó công thức cho mẫu được sử dụng phổ biến hơn.
1. Công thức cho Tổng thể (Population Standard Deviation):
σ = √[ Σ(xᵢ - μ)² / N ]
2. Công thức cho Mẫu (Sample Standard Deviation):
s = √[ Σ(xᵢ - x̄)² / (n - 1) ]
Hãy cùng EBC phân tích chi tiết từng thành phần trong công thức cho Mẫu, là công thức bạn sẽ gặp nhiều nhất:
Ví Dụ Minh Họa
Hãy xem xét một ví dụ đơn giản để thấy rõ cách hoạt động của độ lệch chuẩn. Giả sử chúng ta có lợi nhuận hàng tuần (tính bằng %) của hai cổ phiếu A và B trong 5 tuần qua:
| Tuần |
Lợi nhuận Cổ phiếu A (%) |
Lợi nhuận Cổ phiếu B (%) |
| 1 |
2 |
8 |
| 2 |
3 |
-2 |
| 3 |
4 |
5 |
| 4 |
5 |
1 |
| 5 |
6 |
3 |
Bước 1: Tính lợi nhuận trung bình (x̄)
Bước 2: Tính bình phương độ lệch cho từng cổ phiếu
Cổ phiếu A:
Cổ phiếu B:
Bước 3: Tính phương sai mẫu (s²)
Bước 4: Tính độ lệch chuẩn mẫu (s)
Kết luận từ ví dụ
Mặc dù lợi nhuận trung bình của cổ phiếu A (4%) cao hơn một chút so với cổ phiếu B (3%), nhưng độ lệch chuẩn của cổ phiếu B (3.81%) cao hơn đáng kể so với cổ phiếu A (1.58%). Điều này cho thấy lợi nhuận của cổ phiếu B biến động mạnh hơn rất nhiều.
Một nhà đầu tư ưa thích sự ổn định và rủi ro thấp sẽ chọn cổ phiếu A, trong khi một nhà đầu tư chấp nhận rủi ro cao để tìm kiếm lợi nhuận đột biến có thể quan tâm đến cổ phiếu B. Đây chính là sức mạnh của standard deviation: nó cung cấp một chiều sâu phân tích mà chỉ nhìn vào giá trị trung bình không thể nào thấy được.
Biến Độ Lệch Chuẩn Thành Lợi Thế Cạnh Tranh Trong Đầu Tư
Hiểu định nghĩa và công thức là nền tảng, nhưng biến kiến thức đó thành lợi nhuận mới là mục tiêu cuối cùng của mọi nhà đầu tư. Độ lệch chuẩn không phải là một khái niệm lý thuyết suông; nó là trái tim của nhiều chiến lược và công cụ phân tích tài chính hiện đại. EBC sẽ chỉ cho bạn cách ứng dụng nó một cách thực tế để nâng cao hiệu quả giao dịch và quản lý danh mục đầu tư.
Ứng Dụng Thực Tiễn Số 1: Đo Lường Mức Độ Biến Động (Volatility) Của Thị Trường
Volatility, hay sự biến động, là một thuật ngữ mà bạn nghe thấy hàng ngày trên các kênh tin tức tài chính. Về bản chất, độ lệch chuẩn của chuỗi lợi nhuận của một tài sản chính là thước đo định lượng cho volatility của tài sản đó. Khi các chuyên gia nói rằng thị trường đang có biến động cao, về mặt kỹ thuật, họ đang nói rằng độ lệch chuẩn của lợi nhuận chỉ số thị trường (như S&P 500 hay VN-Index) đang tăng lên.
Lợi ích: Bằng cách theo dõi độ lệch chuẩn lịch sử (historical volatility), nhà đầu tư có thể:
Xác định môi trường thị trường: Trong môi trường biến động thấp (độ lệch chuẩn thấp), các chiến lược đi theo xu hướng (trend-following) có thể hoạt động tốt. Trong môi trường biến động cao (độ lệch chuẩn cao), các chiến lược giao dịch trong biên độ (range-trading) hoặc các chiến lược dựa trên sự đảo chiều trung bình (mean-reversion) có thể hiệu quả hơn.
Điều chỉnh kích thước vị thế: Khi độ lệch chuẩn tăng cao, rủi ro cũng tăng theo. Một nhà quản lý rủi ro thông minh sẽ giảm kích thước vị thế của mình để hạn chế các khoản lỗ tiềm năng. Ngược lại, trong giai đoạn thị trường ổn định, họ có thể tăng kích thước vị thế một cách thận trọng.
Ứng Dụng Thực Tiễn Số 2: Đánh Giá Rủi Ro Và Lợi Nhuận Điều Chỉnh Theo Rủi Ro
Độ lệch chuẩn là thành phần không thể thiếu trong các thước đo hiệu suất đầu tư quan trọng, nổi bật nhất là Tỷ lệ Sharpe (Sharpe Ratio), được phát triển bởi người đoạt giải Nobel William F. Sharpe.
Công thức Tỷ lệ Sharpe: (Lợi nhuận trung bình của danh mục - Lợi nhuận phi rủi ro) / Độ lệch chuẩn của danh mục.
Tỷ lệ Sharpe không chỉ nhìn vào lợi nhuận bạn kiếm được, mà nó đánh giá xem bạn đã phải chấp nhận bao nhiêu rủi ro (đo bằng độ lệch chuẩn) để đạt được lợi nhuận đó. Một tỷ lệ Sharpe cao hơn cho thấy một danh mục đầu tư hoạt động hiệu quả hơn trên cơ sở điều chỉnh theo rủi ro.
Ví dụ:
Ứng Dụng Thực Tiễn Số 3: Nền Tảng Của Các Chỉ Báo Phân Tích Kỹ Thuật Mạnh Mẽ
Một trong những ứng dụng trực quan và phổ biến nhất của độ lệch chuẩn trong phân tích kỹ thuật là chỉ báo Dải Bollinger (Bollinger Bands), được phát minh bởi John Bollinger vào những năm 1980.
Cấu tạo của Dải Bollinger:
Dải Bollinger tạo ra một kênh giá tương đối xung quanh đường trung bình động. Độ rộng của kênh này thay đổi liên tục dựa trên độ lệch chuẩn (volatility) của thị trường.
Cách diễn giải và giao dịch:
Giao dịch với các dải: Giá chạm vào dải trên có thể báo hiệu tình trạng quá mua (overbought), trong khi giá chạm vào dải dưới có thể báo hiệu tình trạng quá bán (oversold). Tuy nhiên, cần kết hợp với các chỉ báo khác để xác nhận tín hiệu.
Việc hiểu rằng Dải Bollinger được xây dựng dựa trên khái niệm thống kê vững chắc là độ lệch chuẩn mang lại cho nhà giao dịch một sự tự tin lớn hơn khi sử dụng công cụ này.
Bạn đã thấy sức mạnh của việc áp dụng độ lệch chuẩn vào phân tích chưa? Để có thể thực hành ngay lập tức những kiến thức này trên biểu đồ thực tế với các chỉ báo như Dải Bollinger, hãy mở ngay một tài khoản demo miễn phí tại EBC. Giao dịch thử nghiệm không rủi ro là cách tốt nhất để bạn biến lý thuyết thành kỹ năng thực chiến trước khi đầu tư bằng tiền thật.
Hướng Dẫn Chi Tiết Cách Tính Toán Và Sử Dụng Độ Lệch Chuẩn
Lý thuyết đã vững, ứng dụng đã rõ, giờ là lúc EBC hướng dẫn bạn các phương pháp thực tế để tính toán độ lệch chuẩn một cách nhanh chóng và chính xác, từ thủ công đến sử dụng các công cụ hiện đại.
Phương Pháp 1: Hướng Dẫn Tính Thủ Công Chi Tiết
Mặc dù trong thực tế ít ai tính thủ công, việc thực hiện một lần sẽ giúp bạn khắc sâu kiến thức. Hãy lấy ví dụ về lợi nhuận hàng tháng (%) của một quỹ đầu tư trong 6 tháng gần nhất: .
1. Tính giá trị trung bình (x̄): (4 + (-1) + 10 + 2 + 5 + 6) / 6 = 26 / 6 ≈ 4.33%
2. Tính độ lệch của từng giá trị so với trung bình và bình phương chúng:
3. Tính tổng các bình phương độ lệch: 0.11 + 28.41 + 32.15 + 5.43 + 0.45 + 2.79 = 69.34
4. Chia cho (n - 1): 69.34 / (6 - 1) = 69.34 / 5 = 13.868 (Đây là phương sai mẫu)
5. Khai căn bậc hai để tìm độ lệch chuẩn: s = √13.868 ≈ 3.72%
Vậy, độ lệch chuẩn của lợi nhuận quỹ đầu tư này là 3.72%.
Phương Pháp 2: Cách Bấm Độ Lệch Chuẩn Trên Máy Tính Casio Phổ Biến
Đối với học sinh, sinh viên và cả những nhà phân tích, máy tính Casio là một công cụ không thể thiếu. Dưới đây là hướng dẫn cho dòng máy phổ biến như Casio FX-570VN PLUS hoặc các dòng tương tự.
Chuyển sang chế độ thống kê:
Nhập dữ liệu:
Ví dụ: Nhập 4=, -1=, 10=, 2=, 5=, 6=.
Xem kết quả:
Sau khi nhập xong, bấm AC để thoát khỏi màn hình nhập liệu.
Bấm SHIFT + 1 (STAT) để vào menu thống kê.
Chọn 4: Var (Các biến).
Tại đây bạn sẽ thấy các ký hiệu:
Trong hầu hết các trường hợp phân tích tài chính, bạn sẽ chọn 4: sx. Bấm 4 rồi bấm =. Kết quả sẽ hiện ra là 3.7239...

Phương Pháp 3: Sử Dụng Hàm Tính Nhanh Trong Excel Hoặc Google Sheets
Đây là phương pháp hiệu quả và được sử dụng rộng rãi nhất trong thực tế khi làm việc với các bộ dữ liệu lớn.
1. Mở Excel hoặc Google Sheets và nhập dữ liệu của bạn vào một cột, ví dụ từ ô A1 đến A6.
2. Chọn một ô trống để hiển thị kết quả.
3. Nhập công thức:
4. Nhấn Enter. Kết quả sẽ được tính toán và hiển thị ngay lập tức.
Phương Pháp 4: Khám Phá Các Công Cụ Tính Độ Lệch Chuẩn Online
Đối với những người cần một phép tính nhanh mà không cần mở phần mềm, có rất nhiều trang web cung cấp công cụ tính toán thống kê online. Bạn chỉ cần tìm kiếm với từ khóa như máy tính độ lệch chuẩn online hoặc standard deviation calculator.
Các công cụ này thường có giao diện rất đơn giản: bạn chỉ cần dán chuỗi dữ liệu của mình vào, phân cách bằng dấu phẩy hoặc dấu cách, và công cụ sẽ trả về ngay lập tức giá trị trung bình, phương sai và độ lệch chuẩn.
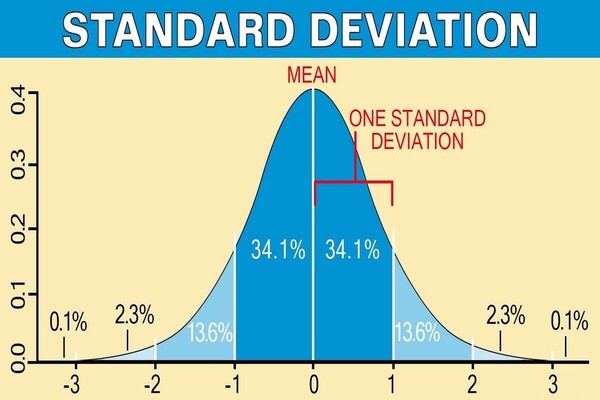
Nâng Tầm Kiến Thức: Từ Độ Lệch Chuẩn Đến Phân Phối Chuẩn
Khi đã làm chủ độ lệch chuẩn, bạn đã sẵn sàng để tiến tới một khái niệm thống kê vô cùng quan trọng trong tài chính: Phân phối chuẩn (Normal Distribution), hay còn gọi là đường cong hình chuông.
Trong một phân phối chuẩn, dữ liệu được phân bố đối xứng quanh giá trị trung bình. Độ lệch chuẩn đóng vai trò quyết định hình dạng của đường cong này. Quy tắc thực nghiệm (Empirical Rule) cho phân phối chuẩn là một kiến thức cực kỳ hữu ích:
Ứng dụng:
Nếu lợi nhuận của một cổ phiếu được giả định là tuân theo phân phối chuẩn với trung bình 10% và độ lệch chuẩn 5%, bạn có thể ước tính rằng có 95% khả năng lợi nhuận năm tới của cổ phiếu này sẽ nằm trong khoảng từ 0% (10% - 25%) đến 20% (10% + 25%).
Đây là một công cụ ước tính xác suất mạnh mẽ để đánh giá các kịch bản có thể xảy ra. Việc tìm hiểu sâu hơn về các khóa học phân tích dữ liệu hoặc thống kê cho tài chính sẽ giúp bạn khai thác tối đa những khái niệm này.
Standard Deviation - Công Cụ Không Thể Thiếu Của Nhà Đầu Tư Thông Minh
Qua bài viết chi tiết này, EBC hy vọng đã làm sáng tỏ câu hỏi standard deviation là gì và trang bị cho bạn một nền tảng kiến thức vững chắc. Độ lệch chuẩn không chỉ là một công thức toán học, nó là một lăng kính để bạn nhìn nhận thị trường một cách rõ ràng và sâu sắc hơn. Nó là ngôn ngữ của rủi ro, là thước đo của sự biến động và là nền tảng cho vô số chiến lược giao dịch và đầu tư thành công.
Từ việc đánh giá một cổ phiếu riêng lẻ, tối ưu hóa danh mục đầu tư, cho đến việc sử dụng các chỉ báo kỹ thuật phức tạp như Dải Bollinger, độ lệch chuẩn luôn hiện diện như một yếu tố cốt lõi. Bằng cách chủ động tìm hiểu và áp dụng nó, bạn đang trang bị cho mình một lợi thế cạnh tranh, chuyển từ việc ra quyết định dựa trên cảm tính sang phân tích dựa trên dữ liệu và xác suất. Đây là bước chuyển mình quan trọng trên con đường trở thành một nhà đầu tư chuyên nghiệp và thành công bền vững.
Hãy bắt đầu hành trình của bạn ngay hôm nay. Kiến thức là sức mạnh, và việc áp dụng kiến thức đó vào thực tế còn mạnh mẽ hơn.
Đừng để những kiến thức quý giá này chỉ nằm trên trang giấy. Hãy biến chúng thành hành động và kinh nghiệm thực tế. Đăng ký ngay một tài khoản giao dịch tại EBC để tiếp cận với nền tảng giao dịch hiện đại, tích hợp đầy đủ các công cụ phân tích kỹ thuật mạnh mẽ.
Bắt đầu giao dịch CFD trên hàng trăm sản phẩm tài chính và áp dụng ngay hiểu biết của bạn về độ lệch chuẩn để quản lý rủi ro và tối ưu hóa lợi nhuận. Giao dịch tại EBC ngay hôm nay để khai phá tiềm năng đầu tư của bạn
Tuyên bố miễn trừ trách nhiệm: Tài liệu này chỉ nhằm mục đích cung cấp thông tin chung và không nhằm mục đích (và cũng không nên được coi là) lời khuyên về tài chính, đầu tư hay các lĩnh vực khác để bạn có thể dựa vào. Không có ý kiến nào trong tài liệu này được coi là khuyến nghị từ EBC hoặc tác giả rằng bất kỳ khoản đầu tư, chứng khoán, giao dịch hay chiến lược đầu tư cụ thể nào phù hợp với bất kỳ cá nhân nào.