Đăng vào: 2025-03-06 Cập nhật vào: 2025-10-29
Fibonacci là gì là câu hỏi về một dãy số phổ quát, nơi mỗi con số là tổng của hai số đứng trước nó, tạo ra một mối liên hệ mật thiết với Tỷ lệ Vàng và được ứng dụng sâu rộng từ quy luật tự nhiên, nghệ thuật cho đến phân tích kỹ thuật trong đầu tư tài chính.
Dãy số Fibonacci là một chuỗi số vô hạn trong toán học, bắt đầu bằng hai phần tử là 0 và 1. Theo quy tắc, phần tử tiếp theo trong chuỗi luôn được tạo ra bằng cách cộng hai phần tử liền trước nó. Do đó, dãy số sẽ có dạng: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, và tiếp tục đến vô tận.
Để áp dụng hiệu quả các công cụ phân tích kỹ thuật dựa trên chuỗi số này, bạn có thể bắt đầu bằng việc mở tài khoản demo tại EBC.
Hãy cùng EBC khám phá sâu hơn về nguồn gốc, các tính chất toán học và cách chuỗi số Fibonacci này định hình thế giới phân tích kỹ thuật cũng như các mô hình trong tự nhiên.
Các ý chính:
Định nghĩa cốt lõi: Dãy Fibonacci là một chuỗi số bắt đầu từ 0 và 1, trong đó mỗi số tiếp theo là tổng của hai số trước đó (ví dụ: 0, 1, 1, 2, 3, 5, 8...).
Tỷ lệ Vàng (Golden Ratio): Tỷ lệ giữa hai số liên tiếp trong dãy Fibonacci xấp xỉ 1.618, một hằng số toán học xuất hiện khắp nơi trong tự nhiên và nghệ thuật.
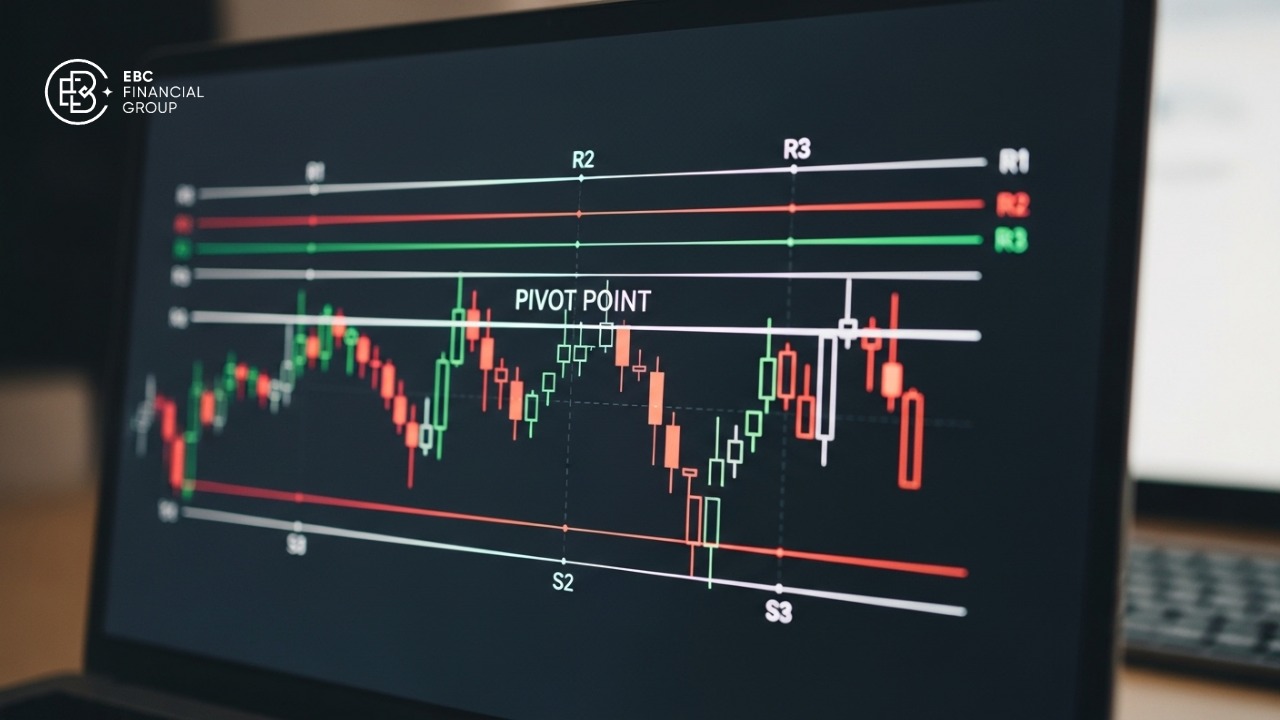
Ứng dụng trong tài chính: Các nhà giao dịch sử dụng các mức Fibonacci Thoái lui (Retracement) và Mở rộng (Extension) để xác định các vùng hỗ trợ, kháng cự và mục tiêu giá tiềm năng.
Hiện diện trong tự nhiên: Cấu trúc của nhiều loài thực vật, động vật, và cả các thiên hà đều tuân theo mô hình xoắn ốc và tỷ lệ của dãy số Fibonacci.
Dãy số Fibonacci không chỉ là một khái niệm toán học thuần túy mà còn là chìa khóa mở ra sự hiểu biết về các quy luật cấu trúc trong vũ trụ. Nền tảng của nó dựa trên một quy luật cộng đơn giản nhưng lại tạo ra những hệ quả vô cùng phức tạp và thú vị, đặc biệt là mối liên hệ với Tỷ lệ Vàng. Hiểu rõ bản chất toán học của dãy số này là bước đầu tiên để có thể ứng dụng nó một cách chính xác và hiệu quả trong nhiều lĩnh vực, từ khoa học tự nhiên đến phân tích thị trường tài chính.
Dãy số Fibonacci được đặt theo tên của nhà toán học người Ý, Leonardo Pisano Bogollo, hay còn được biết đến với biệt danh Fibonacci. Ông sống vào thế kỷ 12 và được coi là một trong những nhà toán học tài ba nhất của thời Trung Cổ. Theo trang Wikipedia, tên gọi Fibonacci được ghép từ chữ Filius Bonacci, có nghĩa là con trai của Bonaccio.
Trong cuốn sách nổi tiếng Liber Abaci (Sách về Phép tính) xuất bản năm 1202, Fibonacci đã giới thiệu dãy số này tới châu Âu. Ông đã mô tả quy luật của dãy số thông qua một bài toán giả định về sự sinh sản của một cặp thỏ. Bài toán đặt ra là: nếu một cặp thỏ (một đực, một cái) được thả vào một cánh đồng, và sau một tháng chúng bắt đầu sinh sản, mỗi tháng đẻ ra một cặp thỏ mới, và các cặp thỏ con cũng theo quy luật tương tự, thì sau một năm sẽ có bao nhiêu cặp thỏ? Lời giải cho bài toán này chính là dãy số 1, 1, 2, 3, 5, 8,... mà ngày nay chúng ta gọi là dãy Fibonacci.
Tuy nhiên, các ghi chép lịch sử cho thấy dãy số này đã được các nhà toán học Ấn Độ cổ đại biết đến từ thế kỷ thứ 6, rất lâu trước thời của Fibonacci. Họ đã sử dụng nó trong các công trình về thi pháp và số liệu Phạn ngữ. Dù vậy, chính Fibonacci là người đã hệ thống hóa và phổ biến nó rộng rãi ở phương Tây, đặt nền móng cho việc nghiên cứu và ứng dụng sâu rộng sau này.
Bản chất của dãy số Fibonacci nằm ở công thức truy hồi đơn giản của nó. Đây là quy tắc nền tảng định hình toàn bộ chuỗi số.
Công thức toán học:Công thức để tính một số Fibonacci bất kỳ trong dãy là: F(n) = F(n-1) + F(n-2)
Trong đó:
F(n) là số Fibonacci ở vị trí thứ n.
Điều kiện ban đầu được xác định là F(0) = 0 và F(1) = 1.
Dựa trên công thức này, chúng ta có thể xây dựng dãy số một cách dễ dàng:
F(2) = F(1) + F(0) = 1 + 0 = 1
F(3) = F(2) + F(1) = 1 + 1 = 2
F(4) = F(3) + F(2) = 2 + 1 = 3
... và cứ thế tiếp diễn.
Mối liên hệ với Tỷ lệ Vàng (Golden Ratio):Một trong những tính chất đáng kinh ngạc và quan trọng nhất của dãy Fibonacci là mối liên hệ mật thiết với Tỷ lệ Vàng, ký hiệu là phi (ϕ), có giá trị xấp xỉ 1.618034. Theo nghiên cứu từ Code Labs Academy, khi bạn lấy một số trong dãy chia cho số đứng ngay trước nó, kết quả sẽ ngày càng tiến gần đến Tỷ lệ Vàng khi các số trong dãy lớn dần.
Ví dụ:
8 / 5 = 1.6
13 / 8 = 1.625
21 / 13 = 1.615
144 / 89 = 1.6179...
Mối quan hệ này không phải là ngẫu nhiên. Tỷ lệ Vàng là một hằng số toán học đặc biệt, được tìm thấy trong nhiều cấu trúc tự nhiên và được coi là tiêu chuẩn cho vẻ đẹp và sự cân đối trong nghệ thuật và kiến trúc. Chính sự liên kết này đã biến dãy Fibonacci từ một bài toán đơn thuần thành một công cụ mạnh mẽ để phân tích các mô hình trong thế giới thực. Ngoài ra, các tỷ lệ khác được suy ra từ dãy số này cũng có ý nghĩa quan trọng, đặc biệt trong phân tích tài chính, chẳng hạn như 0.382 (được tính bằng cách lấy một số chia cho số đứng sau nó hai vị trí) và 0.618 (nghịch đảo của 1.618).
Trong thế giới tài chính, nơi các nhà giao dịch luôn tìm kiếm lợi thế để dự báo biến động giá, dãy số Fibonacci đã trở thành một công cụ phân tích kỹ thuật không thể thiếu. Lý thuyết đằng sau việc ứng dụng này là tâm lý đám đông và các quyết định giao dịch thường tuân theo các quy luật tự nhiên, do đó các mức giá quan trọng cũng có xu hướng tương ứng với các tỷ lệ Fibonacci. Các công cụ như Fibonacci Thoái lui và Mở rộng giúp nhà giao dịch xác định các vùng hỗ trợ, kháng cự tiềm năng, cũng như đặt ra các mục tiêu lợi nhuận một cách có hệ thống và logic hơn thay vì dựa vào cảm tính.
Fibonacci Thoái lui là công cụ phổ biến nhất dựa trên dãy số Fibonacci, được sử dụng để xác định các mức mà tại đó giá có khả năng đảo chiều hoặc tạm dừng sau một xu hướng mạnh. Theo lý thuyết, sau một đợt tăng hoặc giảm giá đáng kể, giá thường có xu hướng điều chỉnh (thoái lui) một phần trước khi tiếp tục xu hướng chính. Các mức thoái lui quan trọng được xác định dựa trên các tỷ lệ Fibonacci.
Các mức tỷ lệ chính:
23.6%: Mức thoái lui nông, cho thấy xu hướng hiện tại rất mạnh.
38.2%: Một mức điều chỉnh phổ biến.
50.0%: Mặc dù không phải là một tỷ lệ Fibonacci chính thức, mức này được đưa vào vì giá thường có xu hướng điều chỉnh về một nửa so với đợt biến động trước đó.
61.8%: Được xem là mức Tỷ lệ Vàng, đây là một trong những mức hỗ trợ/kháng cự mạnh nhất.
78.6%: Mức thoái lui sâu, thường là cơ hội cuối cùng để giá đảo chiều trước khi xu hướng cũ bị phá vỡ.
Hướng dẫn từng bước cách sử dụng:
Xác định xu hướng rõ ràng: Tìm một xu hướng tăng hoặc giảm mạnh trên biểu đồ. Xu hướng được định nghĩa bởi một đỉnh (swing high) và một đáy (swing low) rõ rệt.
Chọn công cụ Fibonacci Retracement: Trên nền tảng giao dịch của bạn, chọn công cụ vẽ Fibonacci Thoái lui.
Vẽ các mức Fibonacci:
Trong một xu hướng tăng: Kéo công cụ từ điểm đáy thấp nhất (swing low) lên điểm đỉnh cao nhất (swing high) của xu hướng.
Trong một xu hướng giảm: Kéo công cụ từ điểm đỉnh cao nhất (swing high) xuống điểm đáy thấp nhất (swing low) của xu hướng.
Phân tích các mức: Các đường ngang được vẽ tự động tại các tỷ lệ Fibonacci sẽ đóng vai trò là các mức hỗ trợ (trong xu hướng tăng) hoặc kháng cự (trong xu hướng giảm) tiềm năng. Các nhà giao dịch sẽ quan sát hành động giá tại các mức này để tìm kiếm tín hiệu vào lệnh.
Ví dụ, nếu giá cổ phiếu tăng từ 50.000 VNĐ lên 80.000 VNĐ và sau đó bắt đầu điều chỉnh giảm, một nhà giao dịch có thể kỳ vọng giá sẽ tìm thấy hỗ trợ tại mức 68.480 VNĐ (thoái lui 38.2%) hoặc 65.000 VNĐ (thoái lui 50%). Để thực hành vẽ các mức Fibonacci này trên biểu đồ thực tế, bạn có thể bắt đầu giao dịch CFD tại EBC.
Công cụ này là một phần không thể thiếu trong bộ kỹ năng của các nhà giao dịch chuyên nghiệp, giúp họ nhận diện các khu vực có khả năng đảo chiều hoặc tiếp diễn xu hướng. Khi thị trường điều chỉnh sau một đợt tăng/giảm mạnh, việc áp dụng phương pháp xác định điểm thoái lui tiềm năng có thể chỉ ra các mức giá mà tại đó xu hướng gốc có thể tiếp tục. Ngược lại, để dự phóng những vùng giá mà thị trường có thể đạt tới sau khi phá vỡ các ngưỡng quan trọng, nhà đầu tư thường tìm hiểu cách tính các mục tiêu giá tiềm năng, từ đó xây dựng chiến lược chốt lời hiệu quả.
Trong khi Fibonacci Thoái lui giúp xác định điểm vào lệnh tiềm năng trong một đợt điều chỉnh, Fibonacci Mở rộng (hay còn gọi là Fibonacci Projection) lại giúp dự báo giá có thể đi xa đến đâu sau khi kết thúc đợt điều chỉnh đó. Công cụ này đặc biệt hữu ích cho việc thiết lập các mục tiêu chốt lời (take-profit).
Các mức tỷ lệ chính:
127.2%: Mục tiêu lợi nhuận đầu tiên, khá thận trọng.
161.8%: Mức Tỷ lệ Vàng, là mục tiêu phổ biến và quan trọng nhất.
261.8%: Mục tiêu xa hơn khi xu hướng rất mạnh.
423.6%: Mục tiêu rất xa, thường xuất hiện trong các đợt bùng nổ giá mạnh mẽ.
Hướng dẫn từng bước cách sử dụng:Công cụ Fibonacci Mở rộng yêu cầu xác định ba điểm trên biểu đồ:
Điểm bắt đầu của xu hướng chính (Điểm 1): Ví dụ, đáy của một đợt tăng giá.
Điểm kết thúc của xu hướng chính (Điểm 2): Đỉnh của đợt tăng giá đó.
Điểm kết thúc của đợt điều chỉnh (Điểm 3): Đáy của đợt thoái lui.
Sau khi xác định ba điểm này, công cụ sẽ chiếu các mức giá tiềm năng trong tương lai. Các nhà giao dịch có thể đặt lệnh chốt lời tại các mức này, ví dụ như chốt một phần vị thế tại mức 161.8% và giữ phần còn lại cho các mục tiêu xa hơn nếu xu hướng tiếp tục mạnh. FPT Shop nhấn mạnh rằng công cụ này có ý nghĩa quan trọng trong việc xác định điểm bán trong xu hướng giảm và điểm mua trong xu hướng tăng, giúp tối ưu hóa lợi nhuận.
Ngoài hai công cụ trên, các nhà giao dịch còn sử dụng các biến thể khác như Fibonacci Fan (Quạt Fibonacci), Fibonacci Arcs (Vòng cung Fibonacci) và Fibonacci Time Zones (Vùng thời gian Fibonacci) để có thêm góc nhìn về các vùng giá và thời gian tiềm năng cho các biến động thị trường.
Ngoài việc được sử dụng độc lập, các tỷ lệ vàng này còn phát huy sức mạnh tối đa khi kết hợp với các lý thuyết và chỉ báo khác. Chẳng hạn, nhiều nhà phân tích thường dùng các cấp độ để củng cố cho việc phân tích cấu trúc sóng thị trường, giúp xác định các điểm kết thúc sóng và bắt đầu sóng mới một cách chính xác hơn. Để trang bị kiến thức toàn diện, việc nắm vững kỹ thuật phân tích đồ thị trong giao dịch ngoại hối là cực kỳ quan trọng, bởi lẽ đây là nền tảng để áp dụng thành công các công cụ nâng cao như tỷ lệ Fibonacci vào thực tiễn.
Sức hấp dẫn của dãy số Fibonacci không chỉ nằm trong các ứng dụng toán học hay tài chính, mà còn ở sự hiện diện đáng kinh ngạc của nó trong thế giới tự nhiên và các kiệt tác nghệ thuật. Mối liên hệ giữa chuỗi số này và Tỷ lệ Vàng (khoảng 1.618) dường như là một mật mã được vũ trụ sử dụng để tạo ra sự cân đối, hài hòa và hiệu quả trong cấu trúc. Từ cách sắp xếp cánh hoa, hình dạng của vỏ sò cho đến cấu trúc của các thiên hà, dấu ấn của Fibonacci ở khắp mọi nơi, cho thấy một quy luật toán học cơ bản đang chi phối vẻ đẹp của vạn vật.
Xoắn ốc Fibonacci (hay xoắn ốc vàng) là một trong những biểu hiện hình học đẹp và phổ biến nhất của dãy số. Hình xoắn ốc này được tạo ra bằng cách vẽ các cung tròn nối các góc đối diện của các hình vuông có cạnh là các số Fibonacci liên tiếp (1, 1, 2, 3, 5, 8,...). Kết quả là một đường xoắn ốc giãn nở một cách hoàn hảo, tuân theo Tỷ lệ Vàng.
Ví dụ trong tự nhiên:
Hoa hướng dương: Số lượng các đường xoắn ốc hạt theo chiều kim đồng hồ và ngược chiều kim đồng hồ trên một bông hoa hướng dương thường là hai số Fibonacci liên tiếp, chẳng hạn như 34 và 55, hoặc 55 và 89. Cách sắp xếp này giúp tối ưu hóa không gian, đảm bảo mỗi hạt nhận được lượng ánh sáng mặt trời và không khí tối đa.
Vỏ ốc anh vũ: Đây là ví dụ kinh điển nhất. Khi cắt dọc một vỏ ốc anh vũ, ta sẽ thấy các ngăn của nó phát triển theo một đường xoắn ốc logarit hoàn hảo, rất gần với xoắn ốc Fibonacci.
Quả dứa và nón thông: Các mắt trên vỏ quả dứa hay các vảy của nón thông cũng được sắp xếp theo hai bộ đường xoắn ốc ngược chiều nhau, và số lượng đường xoắn ốc trong mỗi bộ cũng là các số Fibonacci.
Các cơn bão và thiên hà: Ở quy mô vĩ mô, hình dạng của các cơn bão lớn và thậm chí cả các thiên hà xoắn ốc cũng thường tuân theo mô hình xoắn ốc vàng này. Theo trang Giáo dục & Thời đại, nhiều thứ trong vũ trụ tuân thủ theo tỷ lệ thần thánh này một cách đáng kinh ngạc.
Sự lặp lại của mô hình này cho thấy đây là một giải pháp hiệu quả về mặt cấu trúc và năng lượng mà tự nhiên đã lựa chọn qua hàng triệu năm tiến hóa.
Từ thời cổ đại, các nghệ sĩ và kiến trúc sư đã nhận ra rằng một số tỷ lệ nhất định tạo ra cảm giác hài hòa và thẩm mỹ đặc biệt cho mắt người. Tỷ lệ Vàng, vốn có mối liên hệ trực tiếp với dãy số Fibonacci, chính là nền tảng cho nhiều công trình kiến trúc vĩ đại và các tác phẩm nghệ thuật bất hủ.
Ví dụ trong kiến trúc:
Đền Parthenon, Hy Lạp: Mặt tiền của ngôi đền cổ này được cho là tuân thủ chặt chẽ Tỷ lệ Vàng. Tỷ lệ giữa chiều rộng và chiều cao của nó tạo thành một hình chữ nhật vàng hoàn hảo, mang lại cảm giác cân đối và uy nghi.
Kim tự tháp Giza, Ai Cập: Tỷ lệ giữa chiều cao của một mặt tam giác và một nửa chiều dài cạnh đáy của kim tự tháp cũng xấp xỉ Tỷ lệ Vàng.
Ví dụ trong nghệ thuật:
Leonardo da Vinci: Là một nghệ sĩ và nhà khoa học, da Vinci đã ứng dụng sâu sắc Tỷ lệ Vàng vào các tác phẩm của mình. Bức tranh Mona Lisa nổi tiếng với sự cân đối trên khuôn mặt tuân theo tỷ lệ này. Trong kiệt tác Bữa Tiệc Ly, bố cục sắp xếp các nhân vật và các yếu tố kiến trúc nền cũng được cho là dựa trên Tỷ lệ Vàng để tạo ra sự hài hòa và tập trung vào nhân vật trung tâm.
Nghệ thuật hiện đại: Nhiều nghệ sĩ và nhà thiết kế hiện đại vẫn tiếp tục sử dụng Tỷ lệ Vàng và dãy số Fibonacci để tạo ra các tác phẩm có tính thẩm mỹ cao, từ hội họa, nhiếp ảnh đến thiết kế logo và giao diện người dùng.
Sự hiện diện của Fibonacci trong nghệ thuật và kiến trúc không phải là một sự trùng hợp ngẫu nhiên. Nó cho thấy con người có một cảm nhận bẩm sinh về vẻ đẹp toán học, một vẻ đẹp được tìm thấy trong chính các quy luật cấu tạo nên thế giới xung quanh chúng ta.
Việc hiểu lý thuyết về Fibonacci là quan trọng, nhưng để ứng dụng nó vào thực tế, đặc biệt là trong phân tích tài chính, bạn cần biết cách tính toán và sử dụng các công cụ hỗ trợ. May mắn là ngày nay, có rất nhiều phương pháp để tạo ra dãy số này, từ cách tính thủ công đơn giản, sử dụng các hàm trong lập trình, cho đến các công cụ tích hợp sẵn trên các nền tảng giao dịch chuyên nghiệp. Việc nắm vững cách sử dụng các công cụ này sẽ giúp bạn tiết kiệm thời gian và tăng độ chính xác khi phân tích biểu đồ.
Phương pháp thủ công là cách tốt nhất để hiểu rõ bản chất của dãy số. Quy tắc rất đơn giản: bắt đầu với 0 và 1, sau đó cộng hai số gần nhất để được số tiếp theo.
Dưới đây là bảng minh họa cách tính 15 số Fibonacci đầu tiên:
| Vị trí (n) | Phép tính | Số Fibonacci F(n) |
|---|---|---|
| 0 | - | 0 |
| 1 | - | 1 |
| 2 | F(1) + F(0) = 1 + 0 | 1 |
| 3 | F(2) + F(1) = 1 + 1 | 2 |
| 4 | F(3) + F(2) = 2 + 1 | 3 |
| 5 | F(4) + F(3) = 3 + 2 | 5 |
| 6 | F(5) + F(4) = 5 + 3 | 8 |
| 7 | F(6) + F(5) = 8 + 5 | 13 |
| 8 | F(7) + F(6) = 13 + 8 | 21 |
| 9 | F(8) + F(7) = 21 + 13 | 34 |
| 10 | F(9) + F(8) = 34 + 21 | 55 |
| 11 | F(10) + F(9) = 55 + 34 | 89 |
| 12 | F(11) + F(10) = 89 + 55 | 144 |
| 13 | F(12) + F(11) = 144 + 89 | 233 |
| 14 | F(13) + F(12) = 233 + 144 | 377 |
Đối với những người làm việc trong lĩnh vực khoa học máy tính, dãy số Fibonacci cũng là một bài toán kinh điển để thực hành các thuật toán, đặc biệt là đệ quy. Một hàm đệ quy có thể được viết để tính số Fibonacci thứ n bằng cách gọi chính nó để tính hai số trước đó, phản ánh trực tiếp công thức toán học F(n) = F(n-1) + F(n-2).
Trong giao dịch tài chính, việc tính toán thủ công là không thực tế. Thay vào đó, các nhà giao dịch phụ thuộc vào các công cụ được tích hợp sẵn trên các nền tảng phân tích kỹ thuật như MetaTrader 4/5, TradingView, hay các phần mềm chuyên dụng như Amibroker.
Cách tìm và sử dụng công cụ Fibonacci trên nền tảng giao dịch:
Mở biểu đồ: Chọn một cặp tiền tệ, cổ phiếu, hoặc chỉ số mà bạn muốn phân tích.
Tìm thanh công cụ vẽ: Trên hầu hết các nền tảng, sẽ có một thanh công cụ chứa các đối tượng vẽ kỹ thuật (trendline, kênh giá,...).
Chọn công cụ Fibonacci: Tìm biểu tượng của công cụ Fibonacci (thường là một loạt các đường ngang có ký hiệu %). Các công cụ phổ biến nhất là Fibonacci Retracement và Fibonacci Extension.
Áp dụng lên biểu đồ: Thực hiện các bước vẽ như đã hướng dẫn ở phần trước. Nền tảng sẽ tự động tính toán và hiển thị các mức tỷ lệ Fibonacci chính xác trên biểu đồ giá của bạn.
Ngoài các công cụ tích hợp, bạn có thể dễ dàng tìm thấy một công cụ tính Fibonacci online. Các trang web này cung cấp các máy tính đơn giản, nơi bạn chỉ cần nhập vào vị trí (n) và công cụ sẽ trả về số Fibonacci tương ứng, hoặc thậm chí vẽ biểu đồ các mức thoái lui/mở rộng nếu bạn nhập vào các điểm đỉnh và đáy. Các công cụ này rất hữu ích khi bạn muốn kiểm tra nhanh một con số hoặc thực hiện các tính toán ngoài nền tảng giao dịch chính.
Việc thành thạo các công cụ này cho phép bạn tập trung vào việc phân tích hành động giá tại các mức quan trọng thay vì tốn thời gian cho việc tính toán.
Hiệu quả của việc ứng dụng các chỉ số dựa trên dãy số này còn được nâng cao khi kết hợp với việc hiểu rõ hành động giá trên biểu đồ. Bằng cách quan sát cách giá phản ứng tại các mức then chốt, nhà giao dịch có thể xác nhận các tín hiệu mạnh mẽ hơn. Các mức này thường trùng khớp với những vùng xác định các ngưỡng hỗ trợ và kháng cự, tạo thành các điểm vào/ra lệnh tiềm năng với rủi ro được kiểm soát. Đây là một phương pháp giao dịch mang lại cái nhìn sâu sắc về động thái thị trường.
Qua những phân tích chi tiết, có thể thấy dãy số Fibonacci không chỉ là một khái niệm toán học trừu tượng mà là một nguyên lý hiện hữu sâu sắc trong thế giới xung quanh chúng ta. Từ sự sắp xếp hoàn hảo của tự nhiên đến vẻ đẹp cân đối trong nghệ thuật, và đặc biệt là trong các quy luật tâm lý của thị trường tài chính, Fibonacci cung cấp một lăng kính độc đáo để chúng ta quan sát và diễn giải các mô hình.
Đối với một nhà giao dịch, việc hiểu và áp dụng các công cụ Fibonacci không chỉ là thêm một chỉ báo kỹ thuật vào bộ sưu tập. Đó là việc học cách nhận diện các nhịp điệu của thị trường, xác định các vùng giá có xác suất đảo chiều cao, và thiết lập các mục tiêu lợi nhuận một cách khoa học. Fibonacci không phải là một công cụ thần kỳ đảm bảo chiến thắng, nhưng khi được kết hợp với các phương pháp phân tích khác và một chiến lược quản lý rủi ro chặt chẽ, nó sẽ trở thành một lợi thế mạnh mẽ.
Hãy bắt đầu hành trình khám phá và ứng dụng sức mạnh của dãy số Fibonacci vào chiến lược của bạn bằng cách đăng ký tài khoản tại EBC ngay hôm nay.
Tuyên bố miễn trừ trách nhiệm: Tài liệu này chỉ nhằm mục đích cung cấp thông tin chung và không nhằm mục đích (và cũng không nên được coi là) lời khuyên về tài chính, đầu tư hay các lĩnh vực khác để bạn có thể dựa vào. Không có ý kiến nào trong tài liệu này được coi là khuyến nghị từ EBC hoặc tác giả rằng bất kỳ khoản đầu tư, chứng khoán, giao dịch hay chiến lược đầu tư cụ thể nào phù hợp với bất kỳ cá nhân nào.
