發布日期: 2025年10月31日
不知道有多少人想過,賭錢的時候能夠永遠都贏錢。投資的時候永遠只賺錢。但你知道嗎?確實有這樣神奇的公式,能夠讓人逢賭必贏,投資不賠錢。它就是凱利公式,一個神奇的數學公式。那它到底是什麼?如何保證讓投資人永遠不賠錢?

凱利公式(Kelly Criterion)是一種科學的資金管理工具,用於在多次重複投資或交易中確定每次投入資金的最優比例,以實現長期資產增長最大化。
它強調風險控制與複利成長的平衡,避免「孤注一擲」的風險。
提出者:約翰·拉里·凱利(John Larry Kelly,1923–1965)
推廣者:愛德華·索普(Edward Thorp)-將其成功應用於21點遊戲與股票投資,實現了長期穩定獲利。
1.核心理念:用數學量化“下注的尺度”
它的邏輯非常簡單:
當機率有利時-加大投入
當機率不利時——減少甚至不下注
透過長期重複+ 複利效應,讓資產指數成長。
2.優點
量化風險與效益
利用複利提高長期獲利
避免一把全押導致破產
3.核心用途
凱利公式為投資者提供了一個明確的問題答案:
它適用於:
股票投資
量化交易
外匯與期貨
賭博策略(如21點、運動博彩)
總之,凱利公式提供了最優投資比例f ∗的計算方法,使長期收益最大化,同時避免本金耗盡。

它是一種科學的資金管理方法,核心問題是:在多次重複投資或賭博中,如何確定每次投入資金的比例,以實現資產的長期最大化成長?
1. 基本假設
假設一次投資有兩種可能結果:
贏的機率: p
輸的機率: q=1−p
賭注賠率: b (下注1元,贏了可得到b元利潤)
凱利公式的目標是找到一個最優投資比例f ∗ ,使得在多次重複下注後,資產的對數增長率最大化(即長期複利收益最大)。
2. 公式推導
最優資金比例的推導核心是最大化長期幾何平均收益。
在數學上,這等價於最大化期望對數收益:
對f求導並設導數為零,整理得:
其中:
f ∗ = 每次投資的最優資金比例
b = 投資賠率(獲利金額/ 投資金額)
p = 投資成功機率
q=1−p = 投資失敗機率
結論說明:
當f ∗ > 0 → 可以下注,且比例越高說明機會越有利
當f ∗ ≤ 0 → 不下注,因為期望收益為負
舉例:假設玩拋硬幣遊戲,每局賭注1 元:
猜中→ 贏2 元(b = 2)
猜錯→ 輸1 元
成功機率p=0.5
失敗機率q=0.5
代入公式:
說明:每次投入本金的25%,長期收益最大化。
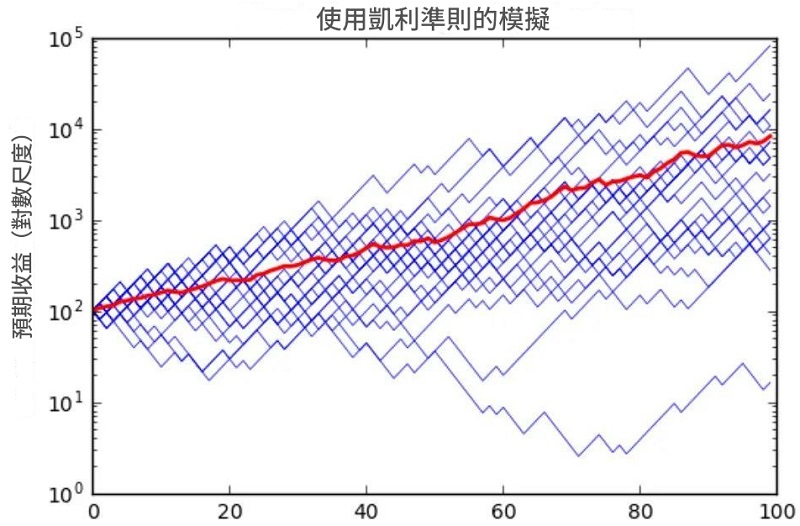
如上圖,在100 次拋硬幣賭局中,
採用凱利公式(紅線)投資的收益曲線明顯優於隨機或全倉操作。
凱利策略:穩健成長
全倉操作:波動劇烈、風險高
推論:
沒有100%勝率的賭局,不值得「All in」:因為一旦失敗將徹底破產
期望收益率為正時,凱利策略最有效:它能量化“下注多少才合理”
多次重複交易才能反映凱利公式優勢:短期內可能波動,但長期收益最優
其是投資和賭博中常用的資金管理方法,用來計算「每次應該投入多少資金」才能讓長期收益最大化。它的故事源自於一位天才科學家的奇思妙想。
1.科學家的靈感
約翰·拉里·凱利(John Larry Kelly, 1923–1965)是美國物理學家,曾在二戰中擔任海軍飛行員。博士畢業後,他進入了著名的貝爾實驗室,與資訊理論之父克勞德·香農共事。
凱利興趣廣泛,既愛研究,又愛冒險。他喜歡橋牌、賽車,還自己改裝車子,是個「科學狂人」。
2.來自電視節目的啟發
凱利的靈感來自一檔熱門電視答題節目-《六萬四千美元的問題》(The $64.000 Question)。
當時,有人利用提前取得的電視訊號進行賭博套利。
凱利因此想到:如果一個人掌握了部分訊息,怎樣才能在反覆下注中讓財富長期增長?
他把這個問題轉化成數學模型,提出了一個著名的凱利公式。
3.從實驗室走進賭場
凱利的論文原名為《資訊理論與賭博》,1956年在貝爾實驗室期刊發表。
起初反響平平,但後來被數學家**愛德華·索普(Edward Thorp)**用於賭場21點。
索普用電腦分析勝率,並用凱利公式決定下注比例。
結果——他真的贏了賭場。
後來,他把經驗寫成暢銷書《戰勝莊家》,並將凱利思想帶入投資領域。
4.現代意義
它的核心思想是:
“在有優勢時多投,沒優勢時少投或不投。”
它能幫助投資者:
控制風險,避免「梭哈」;
利用複利效應,實現長期收益最大化;
合理分配資金,在機率有利時放大優勢。
如今,凱利廣泛應用於:
投資組合管理
量化交易
博彩資金分配
凱利公式告訴我們:投資成功的關鍵不在“贏多少次”,而在“每次投入多少”。
在投資和交易中,科學計算最優部位是實現長期穩定成長的關鍵。凱利公式就是這樣一個核心工具,它能幫助投資人在長期重複交易中:
最大化資金成長率
控制爆倉風險
1.基本原理
適用對象:任何可「贏或輸」的系統,例如股票、期貨、外匯或短線交易。
假設:
勝率: p
虧損機率: q=1−p
損益比(Risk-Reward Ratio): b=平均獲利/平均虧損
則最優倉位比例為:
其中:
f ∗ :每次交易建議投入的資金佔總資產比例
p :交易勝率
q :失敗機率
b :盈虧比
核心理念:
勝率高、盈虧比大→ 可加大部位
勝率低、盈虧比小→ 減少部位或不交易
舉例說明:假設某短線交易者統計如下:
勝率p=0.6
盈虧比b=1
f ∗ = 0.2
▷建議部位:每次投入20%的資金若帳戶資金10 萬元,每次交易投入:
2.盈虧比不同的情況
例如:
勝率p=0.4
盈虧比b=2
f ∗ = 0.1
▷最優部位為10%
儘管勝率下降,高盈虧比仍能支撐正向投入。
3 .應用總結
凱利公式不僅告訴投資者“是否值得交易”,還幫助科學計算最優倉位,實現:
長期複利成長
控制風險與資金曲線波動
避免盲目加倉或全倉操作
它不僅能計算最適投入比例,更能透過風險控制與資金分配優化,幫助投資人在長期投資中實現收益最大化、風險最小化。
1.風險控制最佳化公式
對於風險厭惡型投資者,凱利公式可透過調整公式來控制風險,確保單筆投資失敗時不會造成重大損失。
優化公式:
舉例說明:假設投資人某次交易數據如下:
總資金:100 萬元
每張選擇權最大損失:500 元
風險比例:1%
計算:
投資者最多可持有20張選擇權。
即使全部虧損,總損失也僅為資產的1%。
▷這是一種穩健的資金管理方式,讓投資人即使在極端情況下,也能避免「毀滅性回撤」。
2.多策略資金配置
在實際操作中,許多投資者會同時運行多種策略。
透過分別計算每種策略的凱利資金比例,再綜合調整,就能實現收益與風險的動態平衡。
舉例說明:假設投資人同時執行A、B、C、D、E 五種策略,每種策略的勝率和賠率如下表所示:
| 策略 | 勝率 | 平均虧損 | 平均獲利 | 賠率b |
| A | 50% | -0.28% | 2.49% | 9 |
| B | 75% | -0.74% | 3.27% | 4 |
| C | 50% | -1.23% | 7.30% | 6 |
| D | 75% | -1.95% | 6.51% | 3 |
| E | 92% | -1.84% | 5.91% | 3 |
計算最優資金比例如下:
策略A: f ∗ ≈0.44
策略B: f ∗ ≈0.69
策略C: f ∗ ≈0.42
策略D: f ∗ ≈0.67
策略E: f ∗ ≈0.89
實際資金分配
假設總資金為100萬元,可先平均分配到每種策略(20 萬元),再依最優比例調整:
| 策略 | 平均分配資金 | 調整後投入資金 |
| A | 20 萬 | 8.8 萬 |
| B | 20 萬 | 13.8 萬 |
| C | 20 萬 | 8.4 萬 |
| D | 20 萬 | 13.4 萬 |
| E | 20 萬 | 17.8 萬 |
▷透過這種方式,投資人可以在多策略之間達到平衡,兼顧收益與風險。
3.應用總結
風險控制:透過凱利優化,限定單次最大損失,避免本金被毀滅。
多策略管理:結合不同勝率與賠率,靈活分配資金。
長期複利:實現穩健成長,讓收益在時間中複利放大。
凱利公式的最佳化,不僅是一種數學方法,更是一套科學的資金管理系統。它讓投資人在複雜市場中,做到-有優勢時進取,無優勢時防守。
它雖然能在理論上最大化長期收益,但在真實投資環境中並非「萬能法則」。由於市場的不確定性與人性的複雜性,它在實際運用上存在著多方面的限制。
1.勝率與賠率估計不準確
凱利公式過度依賴精確數據,要求投資人能準確估計:
勝率(p):成功的機率
賠率(b):收益與風險比
然而在現實中,這兩個數據往往無法準確量化。投資者通常依賴:
歷史數據
技術分析
基本面研究
但這些方法都存在著限制──歷史不等於未來,技術指標主觀性強,而基本面又受宏觀因素幹擾。
舉例說明:假設投資人對某股票的估計:
勝率p=0.6
賠率b=1.5
計算得:
若實際勝率為:
勝率p=0.5
賠率b=1.2
計算投資比例應為:
▷誤差將導致過度投資或虧損放大。
2.市場環境動態
凱利公式假設勝率和賠率在多次投資中保持不變,但實際市場(股票、期貨、外匯)會隨時間波動。
實際挑戰
市場波動→ 勝率、賠率即時變化
政策變動、地緣政治→ 突發風險
流動性風險→ 難以如預期平倉
舉例說明:假設外匯交易策略初始:
勝率p=0.5
賠率b=1.2
投資比例:
若市場波動後:
勝率降至p=0.4
賠率降至b=1.0
新的投資比例:
▷理論提示“不應下注”,若繼續操作則可能虧損。
現實結論:凱利策略必須動態調整,而非一成不變。
3.心理因素
投資者情緒可能導致實際操作偏離凱利公式,具體如下:
| 情緒 | 行為 | 結果 |
| 貪婪 | 高估勝率,過度投資 | 承擔過高風險 |
| 恐懼 | 低估勝率,縮小部位 | 錯失機會 |
| 僥倖 | 無視公式,堅持加倉 | 放大虧損 |
▷例如:
凱利策略建議投資20%,但投資人因貪婪實際投入30%。
若市場反轉,下跌損失將大幅超過理論預期。
4.長期重複假設的限制
凱利公式的數學優勢來自於「無限次重複實驗」的前提。然而,投資世界中:
機會有限
資本成本高
情緒與時間窗口受限
舉例說明:假設短期股票交易策略:
勝率p=0.6
賠率b=1.5
凱利計算比例:f ∗ =0.4
若僅有數次機會,投資人應縮小部位至20%,以保持彈性。
▷凱利策略適合長期複利投資,不適合短線遊戲。
凱利公式是一種資金分配框架,不是交易聖杯。它能幫你判斷“應該投多少”,但不能告訴你“何時投、投什麼”。
由於在實際應用中,凱利公式往往帶來較高波動。為平衡風險與效益,許多投資者採用更穩健的「半凱利策略」(Half Kelly)。這種策略透過僅投入凱利計算比例的一半,在控制波動的同時實現穩健成長。
1.半凱利策略的原理
①凱莉公式與波動風險
凱利得出的投資比例f ∗ ,理論上能達到收益最大化,但波動極大。
例如:建議投入40%,若市場短期下跌,帳戶波動會非常明顯。
結論:
凱利追求收益最優,而非風險最小。
對於風險厭惡型或長期投資者而言,需要更穩健的變體。
②半凱利策略的定義
半凱利策略的核心思想:
僅投入凱利公式計算出的比例的一半。
例如,
若凱利策略建議投入40%,則半凱利策略只投入20%。
這樣既能保留成長潛力,又能顯著降低帳戶曲線的波動。
透過降低投入比例,投資人可在保留收益潛力的同時,大幅減少資金曲線的波動幅度。
2.半凱利策略的三大優勢
①降低波動風險
半凱利策略能有效平滑收益曲線,減少短期回檔。
即使連續虧損,損失也較小。
②保持收益潛力
雖然半凱利減少了投資比例,但其長期複合收益通常僅略低於全凱利策略。
更重要的是,較低的波動能讓投資人心理更穩健,不易在短期虧損中放棄策略。
研究顯示:
在實際市場中,半凱利策略的長期回報僅比全凱利低約25%,但波動率下降近50%。
③靈活性與適應性
半凱利策略提供了高度靈活的風險控制機制:
市場波動加大→ 可進一步降至¼ 凱利;
市場趨勢穩定→ 可適度提高至¾ 凱利。
這種靈活機制讓投資人能在不同市況下更從容應對風險。
舉例說明:假設投資人對某檔股票:
勝率p=0.6
賠率b=1.5
計算凱利比例:
全凱利策略:投入40%
半凱利策略:投入20%
假設投資者的總資金為100,000 元,市場出現短期波動,股票價格下跌30%。市場波動下的結果比較:
| 策略類型 | 投入比例 | 投入資金 | 損失金額 | 剩餘資金 |
| 全凱利策略 | 40% | 40000 | 12000 | 88000 |
| 半凱利策略 | 20% | 20000 | 6000 | 94000 |
▷結果:半凱利策略損失更小,資金曲線更平穩。
凱利公式不僅是數學公式,更是科學投資理念:
“在有優勢時進取,無優勢時防守。”
從凱利到索普,再到現代量化交易,它貫穿了數學、機率與實踐的完美結合。掌握凱利,投資不僅學會了計算最優倉位,更學會了在複雜市場中用理性、複利和風險管理實現長期穩健盈利。
投資不是賭博,而是科學與智慧的結合。凱利公式,正是這門科學的指南針。
【EBC平台風險提示及免責條款】:本資料僅供一般參考使用,無意作為(也不應被視為)值得信賴的財務、投資或其他建議。