发布日期: 2025年10月31日
不知道有多少人想过,赌钱的时候能够永远都赢钱。投资的时候永远只赚钱。但你知道吗?确实有这样一个神奇的公式,能够让人逢赌必赢,投资不赔钱。它就是凯利公式,一个神奇的数学公式。那它到底是什么?如何保证让投资者永远不赔钱?

凯利公式(Kelly Criterion)是一种科学的资金管理工具,用于在多次重复投资或交易中确定每次投入资金的最优比例,以实现长期资产增长最大化。
它强调风险控制与复利增长的平衡,避免“孤注一掷”的风险。
提出者:约翰·拉里·凯利(John Larry Kelly,1923–1965)
推广者:爱德华·索普(Edward Thorp)——将其成功应用于21点游戏与股票投资,实现了长期稳定盈利。
1.核心理念:用数学量化“下注的尺度”
它的逻辑非常简单:
当概率有利时——加大投入
当概率不利时——减少甚至不下注
通过长期重复 + 复利效应,让资产实现指数级增长。
2.优点
量化风险与收益
利用复利提高长期盈利
避免一把全押导致破产
3.核心用途
凯利公式为投资者提供了一个明确的问题答案:
它适用于:
股票投资
量化交易
外汇与期货
赌博策略(如21点、体育博彩)
总之,凯利公式提供了最优投资比例 f∗的计算方法,使长期收益最大化,同时避免本金被耗尽。

它是一种科学的资金管理方法,核心问题是:在多次重复投资或赌博中,如何确定每次投入资金的比例,以实现资产的长期最大化增长?
1. 基本假设
假设一次投资有两种可能结果:
赢的概率:p
输的概率:q=1−p
赌注赔率:b(下注1元,赢了可得到 b元利润)
凯利公式的目标是找到一个最优投资比例 f∗,使得在多次重复下注后,资产的对数增长率最大化(即长期复利收益最大)。
2. 公式推导
最优资金比例的推导核心是最大化长期几何平均收益。
在数学上,这等价于最大化期望对数收益:
对f求导并令导数为零,整理得:
其中:
f∗ = 每次投资的最优资金比例
b= 投资赔率(盈利金额 / 投资金额)
p= 投资成功概率
q=1−p = 投资失败概率
结论说明:
当 f∗ > 0 → 可以下注,且比例越高说明机会越有利
当 f∗ ≤ 0 → 不下注,因为期望收益为负
举例说明:假设玩抛硬币游戏,每局赌注 1 元:
猜中 → 赢 2 元(b = 2)
猜错 → 输 1 元
成功概率 p=0.5
失败概率 q=0.5
代入公式:
说明:每次投入本金的 25%,长期收益最大化。
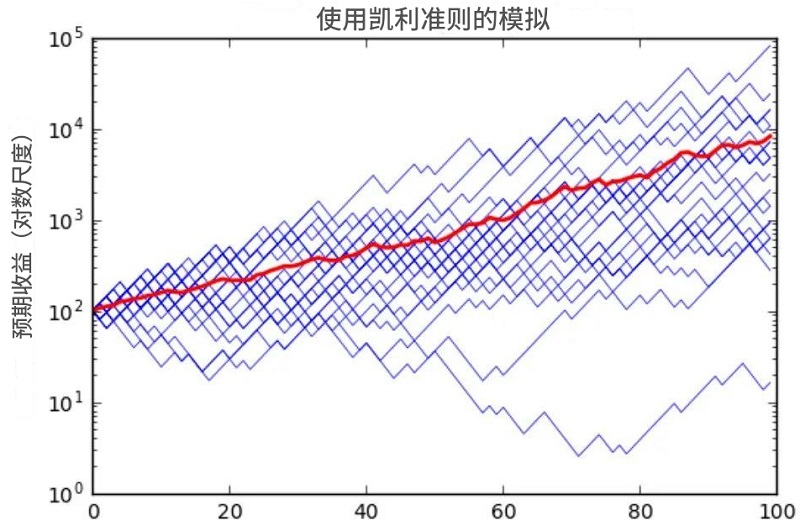
如上图,在 100 次抛硬币赌局中,
采用凯利公式(红线)投资的收益曲线明显优于随机或全仓操作。
凯利策略:稳健增长
全仓操作:波动剧烈、风险高
推论:
没有100%胜率的赌局,不值得“All in”:因为一旦失败将彻底破产
期望收益率为正时,凯利策略最有效:它能量化“下注多少才合理”
多次重复交易才能体现凯利公式优势:短期内可能波动,但长期收益最优
其是投资和赌博中常用的资金管理方法,用来计算“每次应该投入多少资金”才能让长期收益最大化。它的故事源自一位天才科学家的奇思妙想。
1.科学家的灵感
约翰·拉里·凯利(John Larry Kelly, 1923–1965)是美国物理学家,曾在二战中担任海军飞行员。博士毕业后,他进入了著名的贝尔实验室,与信息论之父克劳德·香农共事。
凯利兴趣广泛,既爱研究,又爱冒险。他喜欢桥牌、赛车,还自己改装车子,是个“科学狂人”。
2.来自电视节目的启发
凯利的灵感来自一档热门电视答题节目——《六万四千美元的问题》(The $64.000 Question)。
当时,有人利用提前获取的电视信号进行赌博套利。
凯利因此想到:如果一个人掌握了部分信息,怎样才能在反复下注中让财富长期增长?
他把这个问题转化成数学模型,提出了著名的凯利公式。
3.从实验室走进赌场
凯利的论文最初名为《信息论与赌博》,1956年在贝尔实验室期刊上发表。
起初反响平平,但后来被数学家**爱德华·索普(Edward Thorp)**用于赌场21点。
索普用计算机分析胜率,并用凯利公式决定下注比例。
结果——他真的赢了赌场。
后来,他把经验写成畅销书《战胜庄家》,并将凯利思想带入投资领域。
4.现代意义
它的核心思想是:
“在有优势时多投,没优势时少投或不投。”
它能帮助投资者:
控制风险,避免“梭哈”;
利用复利效应,实现长期收益最大化;
合理分配资金,在概率有利时放大优势。
如今,凯利广泛应用于:
投资组合管理
量化交易
博彩资金分配
凯利公式告诉我们:投资成功的关键不在“赢多少次”,而在“每次投入多少”。
在投资和交易中,科学计算最优仓位是实现长期稳定增长的关键。凯利公式就是这样一个核心工具,它能帮助投资者在长期重复交易中:
最大化资金增长率
控制爆仓风险
1.基本原理
适用对象:任何可“赢或输”的系统,例如股票、期货、外汇或短线交易。
假设:
胜率:p
亏损概率:q=1−p
盈亏比(Risk-Reward Ratio):b=平均盈利/平均亏损
则最优仓位比例为:
其中:
f∗:每次交易建议投入的资金占总资产比例
p:交易胜率
q:失败概率
b:盈亏比
核心理念:
胜率高、盈亏比大 → 可加大仓位
胜率低、盈亏比小 → 减少仓位或不交易
举例说明:假设某短线交易者统计数据如下:
胜率 p=0.6
盈亏比 b=1
f∗=0.2
▷建议仓位:每次投入 20% 的资金
若账户资金10 万元,每次交易投入:
2.盈亏比不同的情况
例如:
胜率 p=0.4
盈亏比 b=2
f∗=0.1
▷最优仓位为10%
尽管胜率下降,但高盈亏比仍能支撑正向投入。
3.应用总结
凯利公式不仅告诉投资者“是否值得交易”,还帮助科学计算最优仓位,实现:
长期复利增长
控制风险与资金曲线波动
避免盲目加仓或全仓操作
它不仅能计算最优投入比例,更能通过风险控制与资金分配优化,帮助投资者在长期投资中实现收益最大化、风险最小化。
1.风险控制优化公式
对于风险厌恶型投资者,凯利公式可通过调整公式来控制风险,确保单笔投资失败时不会造成重大损失。
优化公式:
举例说明:假设投资者某次交易数据如下:
总资金:100 万元
每张期权最大损失:500 元
风险比例:1%
计算:
投资者最多可持有20张期权。
即使全部亏损,总损失也仅为资产的 1%。
▷这是一种稳健的资金管理方式,让投资者即使在极端情况下,也能避免“毁灭性回撤”。
2.多策略资金配置
在实际操作中,许多投资者会同时运行多种策略。
通过分别计算每种策略的凯利资金比例,再综合调整,就能实现收益与风险的动态平衡。
举例说明:假设投资者同时运行 A、B、C、D、E 五种策略,每种策略的胜率和赔率如下表所示:
| 策略 | 胜率 | 平均亏损 | 平均盈利 | 赔率 b |
| A | 50% | -0.28% | 2.49% | 9 |
| B | 75% | -0.74% | 3.27% | 4 |
| C | 50% | -1.23% | 7.30% | 6 |
| D | 75% | -1.95% | 6.51% | 3 |
| E | 92% | -1.84% | 5.91% | 3 |
计算最优资金比例如下:
策略 A:f∗≈0.44
策略 B:f∗≈0.69
策略 C:f∗≈0.42
策略 D:f∗≈0.67
策略 E:f∗≈0.89
实际资金分配
假设总资金为100万元,可先平均分配到每种策略(20 万元),再根据最优比例进行调整:
| 策略 | 平均分配资金 | 调整后投入资金 |
| A | 20 万 | 8.8 万 |
| B | 20 万 | 13.8 万 |
| C | 20 万 | 8.4 万 |
| D | 20 万 | 13.4 万 |
| E | 20 万 | 17.8 万 |
▷通过这种方式,投资者可以在多策略之间实现平衡,兼顾收益与风险。
3.应用总结
风险控制:通过凯利优化,限定单次最大损失,避免本金被毁灭。
多策略管理:结合不同胜率与赔率,灵活分配资金。
长期复利:实现稳健增长,让收益在时间中复利放大。
凯利公式的优化,不仅是一种数学方法,更是一套科学的资金管理体系。它让投资者在复杂市场中,做到——有优势时进取,无优势时防守。
它虽然能在理论上最大化长期收益,但在真实投资环境中并非“万能法则”。由于市场的不确定性与人性的复杂性,它在实际运用中存在多方面的局限。
1.胜率与赔率估计不准确
凯利公式过度依赖精确数据,要求投资者能准确估计:
胜率(p):成功的概率
赔率(b):收益与风险比
然而在现实中,这两个数据往往无法准确量化。投资者通常依赖:
历史数据
技术分析
基本面研究
但这些方法都存在局限——历史并不等于未来,技术指标主观性强,而基本面又受宏观因素干扰。
举例说明:假设投资者对某股票的估计:
胜率 p=0.6
赔率 b=1.5
计算得:
如果实际胜率为:
胜率p=0.5
赔率 b=1.2
计算投资比例应为:
▷误差将导致过度投资或亏损放大。
2.市场环境动态
凯利公式假设胜率和赔率在多次投资中保持不变,但实际市场(股票、期货、外汇)会随时间波动。
实际挑战
市场波动 → 胜率、赔率实时变化
政策变动、地缘政治 → 突发风险
流动性风险 → 难以按预期平仓
举例说明:假设外汇交易策略初始:
胜率 p=0.5
赔率 b=1.2
投资比例:
若市场波动后:
胜率降至 p=0.4
赔率降至 b=1.0
新的投资比例:
▷理论提示“不应下注”,若继续操作则可能亏损。
现实结论:凯利策略必须动态调整,而非一成不变。
3.心理因素
投资者情绪可能导致实际操作偏离凯利公式,具体如下:
| 情绪 | 行为 | 结果 |
| 贪婪 | 高估胜率,过度投资 | 承担过高风险 |
| 恐惧 | 低估胜率,缩小仓位 | 错失机会 |
| 侥幸 | 无视公式,坚持加仓 | 放大亏损 |
▷例如:
凯利策略建议投资 20%,但投资者因贪婪实际投入 30%。
若市场反转,下跌损失将大幅超过理论预期。
4.长期重复假设的局限
凯利公式的数学优势来源于“无限次重复实验”的前提。然而,投资世界中:
机会有限
资本成本高
情绪与时间窗口受限
举例说明:假设短期股票交易策略:
胜率 p=0.6
赔率 b=1.5
凯利计算比例:f∗=0.4
若仅有数次机会,投资者应缩小仓位至 20%,以保持灵活性。
▷凯利策略适合长期复利投资,不适合短线博弈。
凯利公式是一种资金分配框架,不是交易圣杯。它能帮你判断“应该投多少”,但不能告诉你“何时投、投什么”。
由于在实际应用中,凯利公式往往带来较高波动。为平衡风险与收益,许多投资者采用更稳健的“半凯利策略”(Half Kelly)。这种策略通过仅投入凯利计算比例的一半,在控制波动的同时实现稳健增长。
1.半凯利策略的原理
①凯利公式与波动风险
凯利得出的投资比例 f∗,理论上能实现收益最大化,但波动极大。
例如:建议投入 40%,若市场短期下跌,账户波动会非常明显。
结论:
凯利追求收益最优,而非风险最小。
对于风险厌恶型或长期投资者而言,需要更稳健的变体。
②半凯利策略的定义
半凯利策略的核心思想:
仅投入凯利公式计算出的比例的一半。
例如,
若凯利策略建议投入 40%,则半凯利策略只投入 20%。
这样既能保留增长潜力,又能显著降低账户曲线的波动。
通过降低投入比例,投资者可在保留收益潜力的同时,显著减少资金曲线的波动幅度。
2.半凯利策略的三大优势
①降低波动风险
半凯利策略能有效平滑收益曲线,减少短期回撤。
即使连续亏损,损失也较小。
②保持收益潜力
虽然半凯利减少了投资比例,但其长期复合收益通常仅略低于全凯利策略。
更重要的是,较低的波动能让投资者心理更加稳健,不易在短期亏损中放弃策略。
研究表明:
在实际市场中,半凯利策略的长期回报仅比全凯利低约 25%,但波动率下降近 50%。
③灵活性与适应性
半凯利策略提供了高度灵活的风险控制机制:
市场波动加大 → 可进一步降至 ¼ 凯利;
市场趋势稳定 → 可适度提高至 ¾ 凯利。
这种灵活机制让投资者能在不同市况下更从容应对风险。
举例说明:假设投资者对某只股票:
胜率 p=0.6
赔率 b=1.5
计算凯利比例:
全凯利策略:投入 40%
半凯利策略:投入 20%
假设投资者的总资金为100000 元,市场出现短期波动,股票价格下跌 30%。市场波动下的结果对比:
| 策略类型 | 投入比例 | 投入资金 | 损失金额 | 剩余资金 |
| 全凯利策略 | 40% | 40000 | 12000 | 88000 |
| 半凯利策略 | 20% | 20000 | 6000 | 94000 |
▷结果:半凯利策略损失更小,资金曲线更平稳。
凯利公式不仅是一种数学公式,更是一种科学投资理念:
“在有优势时进取,无优势时防守。”
从凯利到索普,再到现代量化交易,它贯穿了数学、概率与实践的完美结合。掌握凯利,投资不仅学会了计算最优仓位,更学会了在复杂市场中用理性、复利和风险管理实现长期稳健盈利。
投资不是赌博,而是科学与智慧的结合。凯利公式,正是这门科学的指南针。
【EBC平台风险提示及免责条款】:本材料仅供一般参考使用,无意作为(也不应被视为)值得信赖的财务、投资或其他建议。