發布日期: 2025年08月29日
更新日期: 2025年10月09日
說到複利,可能很多人都聽說過那些聽起來有點像天方夜譚的故事,比如從100萬變成1.3個億的傳奇。這聽起來是不是有點讓人難以置信?它真的有這么神奇的力量嗎?別急,今天咱們就來好好揭開這背後的神秘面紗,看看它是怎么一步步創造出讓人驚歎的財富增長的!
複利(Compound Interest)是指在計算利息時,不僅本金參與計算,先前累積的利息也會被納入計算範圍,形成新的本金。與簡單利息不同,它透過「利滾利」的方式,使得投資資金在時間的推移下呈指數級增長。其核心在於“利滾利”,即利息不僅是基於本金計算,還包括前期的利息。
舉例說明:假設投資3000元,年報酬率為30%。讓我們來看看它是如何發揮作用的:
| 投資次數 | 初始本金 | 收益(元) | 計算公式 | 總金額(元) |
| 第一次 | 3000元 | 900 | 3000×30% | 3900 |
| 第二次 | 3900元 | 1170 | 3900×30% | 5070 |
| 第三次 | 5070元 | 1521 | 5070×30% | 6591 |
重複以上操作41次,原本的3000元將在它的作用下成長到超過1億。
這驚人的成長,足以讓人深刻領略到它的無窮威力。
因此,複利通常也被稱為“利滾利”“利生利”“錢滾錢”。
信用卡逾期利息其在日常生活中的典型應用之一。
當未能按時還款時,銀行不僅會按日計算逾期利息,還會在每月結算時將這些利息計入本金,再次計算下一期的利息。
隨著時間的推移,逾期利息會像滾雪球一樣越滾越大,甚至可能在不知不覺中超過本金。
這充分體現了複利的「雙面刃」特性:
一方面它能為投資人帶來財富的快速成長,
另一方面如果使用不當,也可能讓人陷入債務的泥沼。
一個古老的故事,讓我們更直觀地感受到它的巨大能量:
相傳,古印度的西薩·班·達依爾發明了國際象棋,國王舍罕為獎勵他,問他需要什麼賞賜。
達依爾提出了一個看似簡單的要求:在棋盤的第一個格子上放1粒麥子,第二個格子放2粒,第三個格子放4粒,以此類推,每個格子的麥子數量都是前一個格子的兩倍,直到填滿棋盤的64個格子。
國王最初認為這不過是區區小事,然而當他真正開始計算時,才發現這個要求簡直是不可能的任務。
因為依照這樣的規則,填滿64個格子所需的麥子數量竟高達1844億億粒,遠遠超出了整個國家的麥子產量。
這個故事生動地展示了「錢滾錢」效應的驚人之處,隨著時間的推移和數量的不斷翻倍,原本微小的數字最終會變成一個令人咋舌的巨大天文數字。
其計算公式是解鎖其財富成長奧秘的關鍵,具體如下:
A :未來的價值(Future Value)。即經過一段時間後,投資將會成長到多少。
P :本金(Principal),也就是最初投入的資金。
r :年利率(Annual Interest Rate),這是決定資金成長速度的關鍵因素之一。
n :每年複利的次數,它決定了利息計算的頻率。
t :投資期間(年),即資金將被投資多久。
舉例說明:假設投資了10000元,年利率為8%,每年「利滾利」一次,投資期間為10年。依公式計算如下:
A=10000×(1.08) 10 ≈21589
說明:
10年後,10,000元的投資將成長為2,1589元,幾乎是原本金的兩倍。
它透過時間的積累,讓資金實現了顯著的成長。
複利頻率,即每年「利滾利」的次數(n),對最終的投資收益有顯著的影響。簡單來說,就是它的頻率越高,資金在單位時間內能夠進行更多的成長循環,進而為投資人帶來更豐厚的回報。
舉例說明:假設同樣的投資10000元,年利率為5%,投資期間為10年,我們分別計算每年一次、每半年一次和每月一次的結果:
| 頻率 | 計算公式 | 最終金額(元) |
| 每年一次 | 10000×1.05 10 | 16288.95 |
| 每半年一次 | 10000×1.025 20 | 16386.16 |
| 每月一次 | 10000×1.004167 120 | 16470.09 |
說明:
隨著頻率的提高,收益也隨之增加。
選擇投資產品時,盡量選「利滾利」頻率高的,以最大化收益。
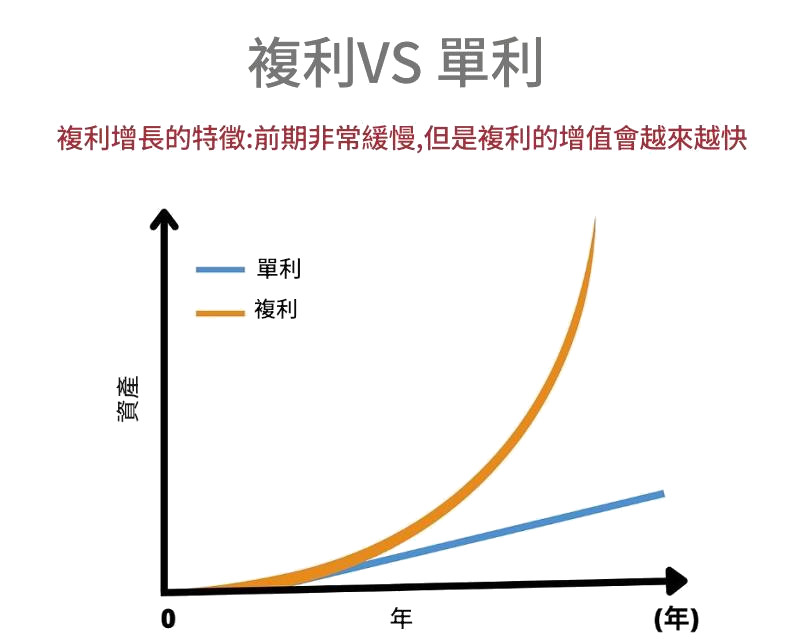
簡單來說,單利是指利息只在本金上計算,不會像複利那樣將利息計入本金再計算利息。
舉例說明:假設投資人有1,000元本金,年報酬率為10%,投資期間為3年。計算結果如下:
1.單利計算結果如下:
| 年份 | 初始金額(元) | 年收益(元) | 累計收益(元) | 總金額(元) |
| 第一年 | 1000 | 100 | 100 | 1100 |
| 第二年 | 1000 | 100 | 200 | 1200 |
| 第三年 | 1000 | 100 | 300 | 1300 |
說明:
每年收益為100元(1000×10%)。
3年後總收益為300元,總金額為1300元。
2.複利計算結果如下:
| 年份 | 初始金額(元) | 收益(元) | 總金額(元) |
| 第一年 | 1000 | 100 | 1100 |
| 第二年 | 1100 | 110 | 1210 |
| 第三年 | 1210 | 121 | 1331 |
說明:
透過「利滾利」 ,三年後獲得了1331元,比單利計算的1300元多出了31元。
雖然在短短3年的時間內,兩者的差距看起來並不大,但隨著時間的推移,這種差距會越來越大。在長期投資中,「錢滾錢」效應將變得極為顯著,能夠為投資者帶來更為可觀的財富成長。
它的威力並非孤立存在,主要依賴三個關鍵要素的協同作用:時間、利率和本金。這三個要素相互關聯、相互影響,共同決定了利滾利的最終效果。
時間是它的最大優勢,也是最關鍵的因素之一。其效果隨著時間的推移而愈發顯著,時間越長,資金的成長潛力就越大。
正如巴菲特所說:「人生就像滾雪球,重要的是發現很濕的雪和很長的坡。」時間就是那個很長的坡,讓的財富在複利的推動下,不斷積累和增長。
舉例說明:假設投資人以4.8%的年利率投資1,000元,投資10年後,20年後的收益如下:
| 年份 | 初始金額(元) | 年利率 | 計算公式 | 未來價值(元) |
| 10年 | 1000 | 4.80% | 1000×(1+0.048) 10 | 1601.03 |
| 20年 | 1000 | 4.80% | 1000×(1+0.048) 20 | 2411.71 |
說明:
較長時間的投資能夠顯著加速財富成長。
可以選擇長期投資,耐心等待加值。
利率是複利的另一個關鍵因素,它決定了資金成長的速度。較高的利率能夠顯著加速資金的成長,為投資者帶來更豐厚的回報。
舉例說明:假設同樣是1萬元的初始投資,A年利率從為10%,投資者B的年利率則為12%,10年後的總金額如下:
| 年利率 | 初始金額 | 年利率 | 計算公式 | 10年後的價值 |
| 10% | 10000元 | 10% | 10000×(1+0.10) 10 | 25937.42元 |
| 12% | 10000元 | 12% | 10000×(1+0.12) 10 | 31058.48元 |
說明:
利率的微小變化在長期內會產生巨大的影響。
選投資產品,重利率合理穩定,求合理高利率促進財富快速成長。
本金是複利的基礎,雖然它的威力主要體現在時間的累積上,但較大的本金也能顯著加速財富的成長。
舉例說明:假設投資者A和B的初始投資分別為1萬元和2萬元,年利率為10% ,10年後的總金額如下:
| 投資者 | 初始金額 | 年利率 | 計算公式 | 10年後的價值 |
| A | 10000元 | 10% | 10000×(1+0.10) 10 | 25937.42元 |
| B | 20000元 | 10% | 20000×(1+0.10) 10 | 51874.84元 |
說明:
本金越大,利滾利起點越高,財富累積越快。
條件允許時,盡量增加初始本金,為財富累積打下堅實基礎。
要最大化其收益,投資人需綜合考慮多因素,採取科學策略。以下方法和注意事項可供參考:
關鍵要點:高利率是它增值的關鍵,優質股票、債券或基金等金融產品可加速財富累積。
風險提示:高報酬率常伴隨高風險,投資人應依自身風險承受能力選產品,平衡風險與收益。
重點:它的最大效應在於時間積累,長期投資能讓資金充分利用複利效應,達到顯著財富成長。
心理調適:長期投資可讓投資人在市場波動中保持冷靜,避免短期決策錯誤,耐心等待其帶來的財富成長。
關鍵要點:定期投資(如每月或每季)是穩健策略,能有效平滑市場波動,降低投資成本。
操作方法:透過“平均成本法”,在市場低谷時買入更多份額,在高峰時買入較少份額,降低平均成本,提高長期收益。
優點:即使市場波動,定期投入資金也能為雪球效應奠定基礎,讓資金在每一次的循環成長中,達到穩定的累積。
關鍵要點:將利息或股利再投資,而非提取,能讓財富持續成長,最大化利滾利效應。
習慣養成:再投資可增加本金,讓利息和股利在利滾利的循環中產生更多收益,投資人應養成此習慣,為財富成長提供強大動力。
長期規劃:它需時間積累,短期難顯優勢,長期投資可讓資金持續成長。投資者要依自身財務和目標定合理期限,堅持執行。
靈活調整:專注於市場動態與產品表現,適時調整策略,保障計畫順利實施。
平衡風險報酬:高報酬率常伴高風險,投資人應依風險承受能力選產品,避免盲目追求高報酬致損失,並注重穩健與合理報酬的平衡。
抵禦通膨侵蝕:通膨會降資金購買力,投資收益需超通膨率才保增值。可選股票、房地產等抗通膨產品,保投資價值。
合理規劃避稅:投資收益要繳稅,影響利滾利效果。投資人要懂稅政策,選稅優惠產品或用政策,合法合規增加收益。
複利,這一金融領域的神奇力量,以其獨特的“利滾利”機制,為投資者帶來了巨大的財富增長潛力。它是一種強大的財富增長工具,但使用需要謹慎和智慧。只有通過科學合理的投資策略和長期的堅持,投資者才能真正發揮它的威力,實現財富的穩健增長,讓自己的財富在時間的長河中不斷積累和壯大。
【EBC平台風險提示及免責條款】:本資料僅供一般參考使用,無意作為(也不應被視為)值得信賴的財務、投資或其他建議。




