2025年08月29日
说到复利，可能很多人都听说过那些听起来有点像天方夜谭的故事，比如从100万变成1.3个亿的传奇。这听起来是不是有点让人难以置信？它真的有这么神奇的力量吗？别急，今天咱们就来好好揭开这背后的神秘面纱，看看它是怎么一步步创造出让人惊叹的财富增长的！
复利（Compound Interest）是指在计算利息时，不仅本金参与计算，之前累积的利息也会被纳入计算范围，形成新的本金。与简单利息不同，它通过“利滚利”的方式，使得投资资金在时间的推移下呈指数级增长。其核心在于“利滚利”，即利息不仅是基于本金计算，还包括前期的利息。
举例说明：假设投资3000元，年回报率为30%。我们来看看它是如何发挥作用的：
| 投资次数 | 初始本金 | 收益（元） | 计算公式 | 总金额（元） |
| 第一次 | 3000元 | 900 | 3000×30% | 3900 |
| 第二次 | 3900元 | 1170 | 3900×30% | 5070 |
| 第三次 | 5070元 | 1521 | 5070×30% | 6591 |
重复以上操作41次，原本的3000元将在它的作用下增长到超过1亿。
这惊人的增长，足以让人深刻领略到它的无穷威力。
因此，复利通常也被称为“利滚利”“利生利”“钱滚钱”。
信用卡逾期利息其在日常生活中的典型应用之一。
当未能按时还款时，银行不仅会按日计算逾期利息，还会在每月结算时将这些利息计入本金，再次计算下一期的利息。
随着时间的推移，逾期利息会像滚雪球一样越滚越大，甚至可能在不知不觉中超过本金。
这充分体现了复利的“双刃剑”特性：
一方面它能为投资者带来财富的快速增长，
另一方面如果使用不当，也可能让人陷入债务的泥沼。
一个古老的故事，让我们更加直观地感受到它的巨大能量：
相传，古印度的西萨·班·达依尔发明了国际象棋，国王舍罕为奖励他，问他需要什么赏赐。
达依尔提出了一个看似简单的要求：在棋盘的第一个格子上放1粒麦子，第二个格子放2粒，第三个格子放4粒，以此类推，每个格子的麦子数量都是前一个格子的两倍，直到填满棋盘的64个格子。
国王最初认为这不过是区区小事，然而当他真正开始计算时，才发现这个要求简直是不可能完成的任务。
因为按照这样的规则，填满64个格子所需的麦子数量竟高达1844亿亿粒，远远超出了整个国家的麦子产量。
这个故事生动地展示了“钱滚钱”效应的惊人之处，随着时间的推移和数量的不断翻倍，原本微小的数字最终会变成一个令人咋舌的巨大天文数字。
其计算公式是解锁其财富增长奥秘的关键，具体如下：
A：未来的价值（Future Value）。即经过一段时间后，投资将增长到多少。
P：本金（Principal），也就是最初投入的资金。
r：年利率（Annual Interest Rate），这是决定资金增长速度的关键因素之一。
n：每年复利的次数，它决定了利息计算的频率。
t：投资期限（年），即资金将被投资多长时间。
举例说明：假设投资了10000元，年利率为8%，每年“利滚利”一次，投资期限为10年。根据公式计算如下：
A=10000×(1.08)10≈21589
说明：
10年后，10000元的投资将增长为21589元，几乎是原本金的两倍。
它通过时间的积累，让资金实现了显著的增长。
复利频率，即每年“利滚利”的次数(n)，对最终的投资收益有着显著的影响。简单来说，就是它的频率越高，资金在单位时间内能够进行更多的增长循环，从而为投资者带来更为丰厚的回报。
举例说明：假设同样的投资10000元，年利率为5%，投资期限为10年，我们分别计算每年一次、每半年一次和每月一次的结果：
| 频率 | 计算公式 | 最终金额（元） |
| 每年一次 | 10000×1.0510 | 16288.95 |
| 每半年一次 | 10000×1.02520 | 16386.16 |
| 每月一次 | 10000×1.004167120 | 16470.09 |
说明：
随着频率的提高，收益也相应增加。
选择投资产品时，尽量选“利滚利”频率高的，以最大化收益。
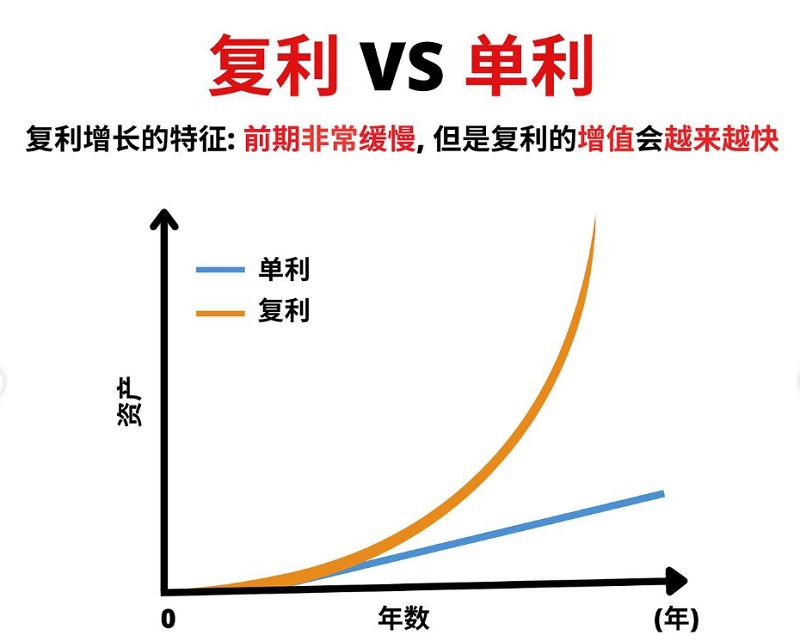
简单来说，单利是指利息只在本金上计算，不会像复利那样将利息计入本金再次计算利息。
举例说明：假设投资者有1000元本金，年回报率为10%，投资期限为3年。计算结果如下：
1.单利计算结果如下：
| 年份 | 初始金额（元） | 年收益（元） | 累计收益（元） | 总金额（元） |
| 第一年 | 1000 | 100 | 100 | 1100 |
| 第二年 | 1000 | 100 | 200 | 1200 |
| 第三年 | 1000 | 100 | 300 | 1300 |
说明：
每年收益为100元(1000×10%)。
3年后总收益为300元，总金额为1300元。
2.复利计算结果如下：
| 年份 | 初始金额（元） | 收益（元） | 总金额（元） |
| 第一年 | 1000 | 100 | 1100 |
| 第二年 | 1100 | 110 | 1210 |
| 第三年 | 1210 | 121 | 1331 |
说明：
通过“利滚利”，三年后获得了1331元，比单利计算的1300元多出了31元。
虽然在短短3年的时间内，两者的差距看起来并不大，但随着时间的推移，这种差距会越来越大。在长期投资中，“钱滚钱”效应将变得极为显著，能够为投资者带来更为可观的财富增长。
它的威力并非孤立存在，主要依赖于三个关键要素的协同作用：时间、利率和本金。这三个要素相互关联、相互影响，共同决定了利滚利的最终效果。
时间是它的最大优势，也是最为关键的因素之一。其效果随着时间的推移而愈发显著，时间越长，资金的增长潜力就越大。
正如巴菲特所说：“人生就像滚雪球，重要的是发现很湿的雪和很长的坡。”时间就是那个很长的坡，让的财富在复利的推动下，不断积累和增长。
举例说明：假设投资者以4.8%的年利率投资1000元，投资10年后，20年后的收益如下：
| 年份 | 初始金额（元） | 年利率 | 计算公式 | 未来价值（元） |
| 10年 | 1000 | 4.80% | 1000×(1+0.048)10 | 1601.03 |
| 20年 | 1000 | 4.80% | 1000×(1+0.048)20 | 2411.71 |
说明：
较长时间的投资能够显著加速财富增长。
可以选择长期投资，耐心等待增值。
利率是复利的另一个关键因素，它决定了资金增长的速度。较高的利率能够显著加速资金的增长，为投资者带来更为丰厚的回报。
举例说明：假设同样是1万元的初始投资，A年利率从为10%，投资者B的年利率则为12%，10年后的总金额如下：
| 年利率 | 初始金额 | 年利率 | 计算公式 | 10年后的价值 |
| 10% | 10000元 | 10% | 10000×(1+0.10)10 | 25937.42元 |
| 12% | 10000元 | 12% | 10000×(1+0.12)10 | 31058.48元 |
说明：
利率的微小变化在长期内会产生巨大的影响。
选投资产品，重利率合理稳定，求合理高利率促财富快增长。
本金是复利的基础，虽然它的威力主要体现在时间的积累上，但较大的本金也能显著加快财富的增长。
举例说明：假设投资者A和B的初始投资分别为1万元和2万元，年利率为10%，10年后的总金额如下：
| 投资者 | 初始金额 | 年利率 | 计算公式 | 10年后的价值 |
| A | 10000元 | 10% | 10000×(1+0.10)10 | 25937.42元 |
| B | 20000元 | 10% | 20000×(1+0.10)10 | 51874.84元 |
说明：
本金越大，利滚利起点越高，财富积累越快。
条件允许时，尽量增加初始本金，为财富积累打下坚实基础。
要最大化其收益，投资者需综合考虑多因素，采取科学策略。以下方法和注意事项可供参考：
关键要点：高利率是它增值的关键，优质股票、债券或基金等金融产品可加速财富积累。
风险提示：高报酬率常伴高风险，投资者应依自身风险承受能力选产品，平衡风险与收益。
要点：它的最大效应在于时间积累，长期投资能让资金充分利用复利效应，实现显著财富增长。
心理调适：长期投资可让投资者在市场波动中保持冷静，避免短期决策失误，耐心等待其带来的财富增长。
关键要点：定期投资(如每月或每季度)是稳健策略，能有效平滑市场波动，降低投资成本。
操作方法：通过“平均成本法”，在市场低谷时买入更多份额，在高峰时买入较少份额，降低平均成本，提高长期收益。
优势：即使市场波动，定期投入资金也能为雪球效应奠定基础，让资金在每一次的循环增长中，实现稳定的积累。
关键要点：将利息或股息再投资，而非提取，能让财富继续增长，最大化利滚利效应。
习惯养成：再投资可增加本金，让利息和股息在利滚利的循环中产生更多收益，投资者应养成此习惯，为财富增长提供强大动力。
长期规划：它需时间积累，短期难显优势，长期投资可让资金持续增长。投资者要依自身财务和目标定合理期限，坚持执行。
灵活调整：关注市场动态和产品表现，适时调整策略，保障计划顺利实施。
平衡风险收益：高回报率常伴高风险，投资者应依风险承受能力选产品，避免盲目追求高回报致损失，注重稳健与合理回报的平衡。
抵御通胀侵蚀：通胀会降资金购买力，投资收益需超通胀率才保增值。可选股票、房地产等抗通胀产品，保投资价值。
合理规划避税：投资收益要缴税，影响利滚利效果。投资者要懂税收政策，选税收优惠产品或用政策，合法合规增收益。
复利，这一金融领域的神奇力量，以其独特的“利滚利”机制，为投资者带来了巨大的财富增长潜力。它是一种强大的财富增长工具，但使用需要谨慎和智慧。只有通过科学合理的投资策略和长期的坚持，投资者才能真正发挥它的威力，实现财富的稳健增长，让自己的财富在时间的长河中不断积累和壮大。
