发布日期: 2025年10月07日
更新日期: 2025年10月09日
收益与风险,是金融投资中永恒的主题。只有当两者达到平衡,投资者才能在可控风险下实现理想回报。在众多投资产品中,如何选择“性价比”最高的组合?答案就在于一个核心指标——夏普值(Sharpe Ratio)。作为评估风险调整后收益的重要工具,夏普指数能帮助投资者量化风险与收益的关系,从而做出更科学、更理性的投资决策。
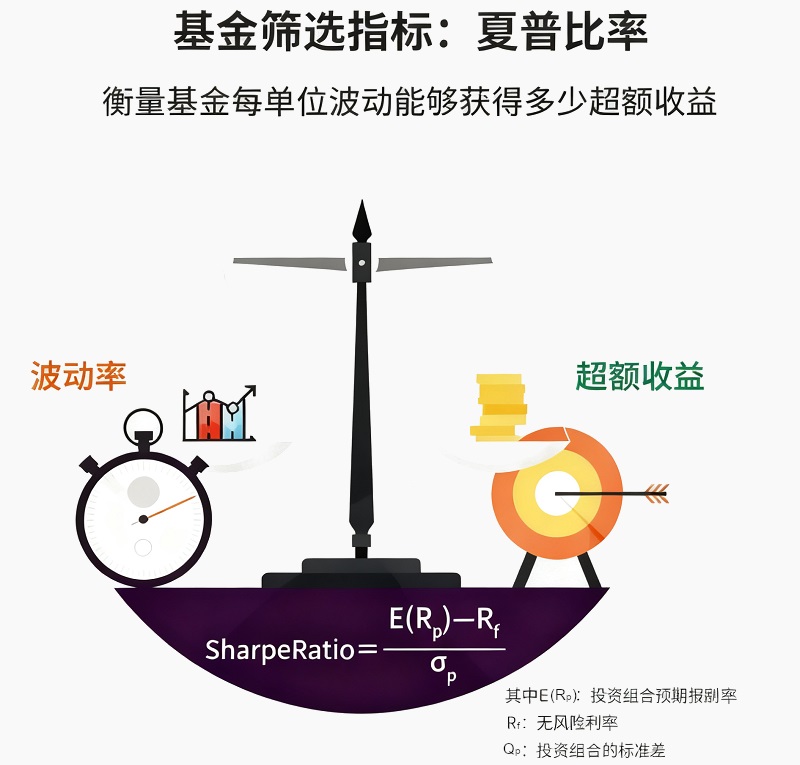
夏普值也就是人们常说的夏普比率(Sharpe Ratio),由美国经济学家 威廉·夏普(William F. Sharpe) 于1966年提出,是投资界最常用的风险调整收益指标。它回答了一个关键问题:
“投资者每承担一单位风险,能获得多少额外收益?”
夏普指标公式如下:
其中:
E(Rp):投资组合的预期回报率(通常为年化收益率)
Rf:无风险利率(一般参考国债收益率,如美国10年期国债)
σp:投资组合收益率的标准差(即波动率,用于衡量风险)
💬 通俗理解
分子:代表“多赚了多少”(超额收益)
分母:代表“承担了多少风险”
结果:代表“单位风险获得的回报”
简单来说,夏普值越高,意味着在同样风险下,投资组合能带来更多收益。因此,它成为了众多投资者挑选投资产品或组合的筛选指标。

我们用一个简单例子来说明:
假设某投资组合的数据如下:
年化收益率:15%
无风险利率:3%
年化波动率(标准差):10%
计算过程如下:
| 项目 | 数值 | 说明 |
| 年化收益率 | 15% | 投资组合的年化收益率 |
| 无风险利率 | 3% | 基准收益 |
| 年化波动率 | 10% | 投资组合的标准差,衡量风险 |
| 超额收益率 | 12% | 15% - 3%,即超出无风险部分 |
| 夏普比率 | 1.2 | 12% / 10% |
结论:这意味着该投资组合在承担“1单位风险”的情况下,能获得“1.2单位的额外回报”。
在投资世界中,“高收益伴随高风险”几乎是铁律。然而,聪明的投资者并不盲目追求高收益,而是追求风险调整后的高收益。这正是夏普值(Sharpe Ratio)存在的意义。要理解它,我们需要先掌握三个核心概念:
1. 无风险利率(Risk-Free Rate)
无风险利率是投资者在不承担任何风险的情况下可以获得的收益。
通常以美国10年期国债收益率作为参考,因为国债违约风险极低。
举例说明:如果美国10年期国债收益率为 2%,
这意味着把资金投入国债,可以稳定获得 2% 年化收益,
同时本金几乎没有风险。
公式意义:
它代表了“安全收益”的基准线,
所有高于无风险利率的收益,都是“承担风险的回报”。
2. 标准差(Standard Deviation)
标准差用于衡量投资组合收益的波动性,也就是“风险”的量化指标。
波动越大,代表收益起伏越剧烈,风险也越高。
举例说明:假设某投资组合近五个月的月收益率如下:
10%、-5%、15%、-10%、20%
那么收益上下起伏很大,
这意味着其标准差较高,投资风险相对更大。
简而言之:
标准差越高,说明收益越不稳定;
标准差越低,说明收益更平稳可预期。
3. 超额收益(Excess Return)
超额收益是投资者在超出无风险利率部分所获得的回报,
也就是“冒风险赚到的额外钱”。
举例说明:若投资组合年化收益率为 15%,而无风险利率为 3%,
那么超额收益 = 15% - 3% = 12%。
意义:
这 12% 就是投资者为了承担风险而获得的“风险溢价”。
| 指标 | 含义 | 示例 | 对应风险层级 |
| 无风险利率 (Rf) | 无风险下的基准收益 | 美国10年期国债 2% | 无风险 |
| 标准差 (σp) | 收益波动的程度 | 收益波动大 → 风险高 | 高风险 |
| 超额收益 (E(Rp)-Rf) | 超出无风险利率的部分 | 15%-3%=12% | 风险溢价 |
在投资世界中,高收益并不一定意味着好投资。关键在于:为这份收益,承担了多大的风险?这正是夏普值(Sharpe Ratio)的核心意义——通过风险调整后的收益,帮助投资者找到最优性价比的投资组合。
1.收益与风险的平衡
夏普比率的最大优势在于,它同时考虑了收益与风险两个维度。
判断逻辑:
当两只基金收益相同 → 夏普比率更高的基金风险更低
当两只基金风险相同 → 夏普比率更高的基金收益更高
也就是说,夏普比率高的投资,更能在风险可控的前提下,实现稳定增长。
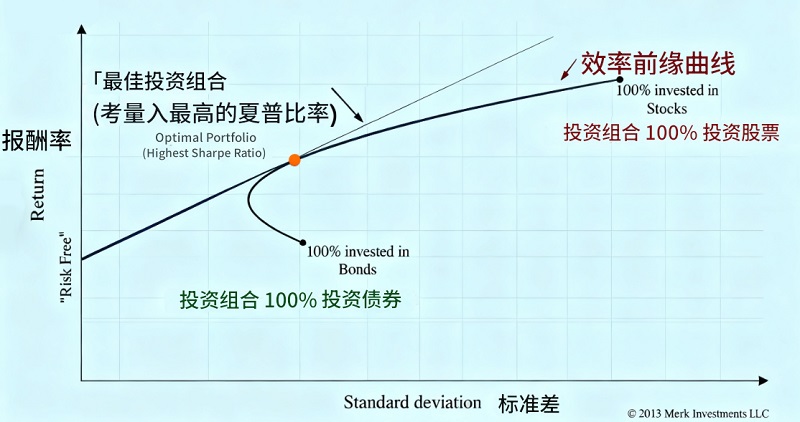
2.比较不同投资组合的绩效
夏普比率还可以作为不同投资组合之间的对比指标,帮助投资者判断哪一项投资在风险调整后表现更佳。
举例说明:假设投资者面临两个投资组合A和B,它们的预期收益率、无风险利率和标准差如下:
投资组合A:预期收益率18%,无风险利率3%,标准差12%
投资组合B:预期收益率16%,无风险利率3%,标准差8%
比较这两个投资组合的绩效,计算如下:
| 项目 | 投资组合A | 投资组合B |
| 预期收益率 | 18% | 16% |
| 无风险利率 | 3% | 3% |
| 标准差 | 12% | 8% |
| 超额收益率 | 15% | 13% |
| 夏普比率 | 1.25 | 1.625 |
计算结果:
夏普比率A = (18% - 3%) ÷ 12% = 1.25
夏普比率B = (16% - 3%) ÷ 8% = 1.625
结果:
虽然投资组合A的收益率更高,但其波动性(风险)更大。
投资组合B的夏普比率更高,说明它能在更低风险下实现更高风险调整收益。
从性价比角度看,B 是更高效、更稳健的投资选择。
3.评估投资组合的风险调整收益
夏普比率不仅用于比较基金之间的表现,更是投资者自我审视投资策略的有力工具。
逻辑解读:
若投资组合收益高但夏普比率低 → 收益与风险不匹配,需警惕波动。
若投资组合收益适中但夏普比率高 → 风险调整后表现优秀,更稳健可靠。
举例说明:假设两位投资者:
投资者甲:年化收益 20%,波动率 15%,夏普比率 1.13
投资者乙:年化收益 12%,波动率 6%,夏普比率 1.5
尽管甲的收益更高,但乙的夏普比率更高,意味着乙在承担更小风险的情况下,获得了更高的风险调整回报。
| 对比维度 | 普通收益率 | 夏普比率 |
| 关注点 | “赚了多少” | “赚得值不值” |
| 考虑风险 | ❌ 无 | ✅ 有 |
| 可比性 | 仅限同类收益 | 可跨资产比较 |
| 投资指导性 | 一般 | ⭐ 高 |
一句话总结:
夏普值是评估投资效率的核心工具。
它让投资者明白:高收益不重要,稳健收益才更有价值。
夏普比率是衡量风险调整后收益的重要指标。它的数值越高,代表单位风险下能获得的额外收益越多。但“多少才算好”?下面我们通过标准区间与实际案例来全面解读:
①<1:风险大于收益,投资性价比低
当夏普值低于1时,说明投资的超额收益不足以补偿风险。
投资者承担了较大的波动,却没有得到相应的回报。
举例说明:假设一个投资组合的年化收益率为8%,无风险利率为3%,年化波动率为10%。计算如下:
| 项目 | 数值 | 说明 |
| 资产年化收益率 | 8% | 投资组合收益 |
| 无风险利率 | 3% | 基准收益 |
| 年化波动率 | 10% | 风险水平 |
| 超额收益率 | 5% | 8% - 3% |
| 夏普比率 | 0.5 | 5% / 10% |
结果:夏普比率0.5<1,表示风险较高但收益偏低,长期投资性价比不佳。
②≈ 1:收益略高于风险,可接受
当夏普比率接近 1,代表投资组合在风险与收益之间保持了基本平衡。
适合风险承受力中等的投资者。
举例说明:假设一个投资组合的年化收益率为10%,无风险利率为3%,年化波动率为7%。计算如下:
| 项目 | 数值 | 说明 |
| 资产年化收益率 | 10% | 投资组合收益 |
| 无风险利率 | 3% | 基准收益 |
| 年化波动率 | 7% | 风险水平 |
| 超额收益率 | 7% | 10% - 3% |
| 夏普比率 | 1 | 7% / 7% |
结果解读:收益略高于风险,整体表现稳定,适合追求稳健增长的投资者。
③> 1:风险调整后收益优良
当夏普比率超过 1,说明超额收益明显超过风险,
这类投资组合通常被视为“高性价比”的选择。
举例说明:假设一个投资组合的年化收益率为15%,无风险利率为3%,年化波动率为10%。计算如下:
| 项目 | 数值 | 说明 |
| 资产年化收益率 | 15% | 投资组合收益 |
| 无风险利率 | 3% | 基准收益 |
| 年化波动率 | 10% | 风险水平 |
| 超额收益率 | 12% | 15% - 3% |
| 夏普比率 | 1.2 | 12% / 10% |
结果:夏普比率 1.2 > 1,风险调整后收益表现优异,体现了良好的投资管理与资产配置能力。
④> 2:表现极佳,顶级投资组合
当夏普比率超过 2 时,代表投资者获得了极高的风险回报比。
这类投资策略往往来源于成熟的量化模型或顶级基金经理操作。
举例说明:假设一个投资组合的年化收益率为20%,无风险利率为3%,年化波动率为10%。计算如下:
| 项目 | 数值 | 说明 |
| 资产年化收益率 | 20% | 投资组合收益 |
| 无风险利率 | 3% | 基准收益 |
| 年化波动率 | 10% | 风险水平 |
| 超额收益率 | 17% | 20% - 3% |
| 夏普比率 | 1.7 | 17% / 10% |
结果解读:
虽然示例值略低于 2,但已接近“极佳表现”区间。
若持续维持高夏普比率,说明投资组合具备强大的风险控制能力。
⑤负数:收益低于无风险利率,应避免
当夏普值为负时,意味着投资回报甚至不如无风险资产,不仅没有获得额外收益,还可能存在亏损。
举例说明:假设一个投资组合的年化收益率为2%,无风险利率为3%,年化波动率为10%。计算如下:
| 项目 | 数值 | 说明 |
| 资产年化收益率 | 2% | 投资组合收益 |
| 无风险利率 | 3% | 基准收益 |
| 年化波动率 | 10% | 风险水平 |
| 超额收益率 | -1% | 2% - 3% |
| 夏普比率 | -0.1 | -0.1 |
结果:夏普比率为负,代表投资表现劣于国债,应及时止损或优化资产配置。
| 夏普比率区间 | 风险回报关系 | 投资建议 |
| < 0 | 收益低于无风险利率 | 🚫 避免投资 |
| 0 – 1 | 收益不足以覆盖风险 | ⚠️ 谨慎参与 |
| ≈ 1 | 风险与收益平衡 | ✅ 可接受 |
| 1 – 2 | 风险调整后收益优良 | 🌟 值得投资 |
| > 2 | 高质量投资组合 | 🚀 表现卓越 |
提示:夏普值没有“绝对标准”,更适合在同类资产或相似基金之间比较。例如,比较两只科技基金或两种量化策略时,才具有参考意义。
1.假设条件的限制
问题: 夏普比率假设投资组合收益服从“正态分布”。
现实: 实际市场中,收益往往呈现偏态(Skewness)或厚尾(Fat Tail),极端事件(暴涨/暴跌)发生频率更高。
解释:
这种情况下,夏普比率可能低估极端风险,使投资者误判安全性。
举例说明:
2020年疫情期间,许多基金短期大幅下跌,这种“黑天鹅事件”在正态假设下几乎不可能出现,因此夏普比率无法准确反映真实风险。
2.时间跨度的影响
问题:夏普值对时间窗口极为敏感,不同时间段可能得出完全不同的结果。
解释:
在比较不同基金时,应确保数据区间一致,否则结论缺乏可比性。
例子:
若取 2010–2022 年 的数据,股票型基金可能表现最佳;
但若取 1987–2022 年 的区间,债券或黄金可能胜出。
3.无风险利率的选择
问题: 无风险利率(Risk-Free Rate)的设定直接影响夏普比率结果。
解释:
不同经济环境下,无风险利率波动较大(如美国10年期国债从2%升至3%)。
例子:
若投资组合收益率为10%,标准差8%,则:
当无风险利率=2%,夏普比率=1.00
当无风险利率=3%,夏普比率=0.875
同样的基金,仅因利率变化,性价比评价就发生改变。
4.数据的局限性
问题: 夏普值基于历史数据,而历史并不等于未来。
解释:
市场趋势、政策与经济周期变化可能导致未来表现大幅不同。
例子:
某基金过去10年夏普比率为1.6,看似稳定,但未来经济环境若转弱,其风险收益结构可能下滑至1.0以下。
了解夏普值是什么只是第一步,真正关键的是如何“正确使用”。以下是基金投资者在实务中应遵循的四项核心建议。
1.选择合适的数据周期
建议1:至少回测 7–10 年
确保数据覆盖不同市场环境(牛市 + 熊市),避免只看单边上涨期。
建议2:避免仅使用多头年份数据
上涨周期中的夏普比率偏高,容易误导判断。
只有在完整市场周期下回测,才能评估策略的真实抗风险能力。
2.滚动测试(Rolling Test)
操作方法:将历史收益分段计算夏普比率,观察其随时间变化的稳定性。
例子:若一只基金在不同时间段夏普比率波动极大,说明策略可能过于依赖特定行情。
3.同类资产比较
原则:同类基金之间比较才有意义。
股票基金 ↔ 股票基金
债券基金 ↔ 债券基金
跨资产类别比较会因风险特征差异而失真。
股票基金夏普比率通常高于债券基金,但这并不意味着“更好”,而是承担了更高波动风险。
4.结合其他指标
索提诺比率(Sortino Ratio):关注下行风险
崔纳比率(Treynor Ratio):考虑系统性风险
最大回撤(Max Drawdown)、VaR/CVaR:评估极端风险
建议:不要单独依赖夏普值,应综合多维度风险指标形成完整风险画像。
夏普值是评估风险调整收益的核心工具,让投资者明白:
高收益不等于高性价比
稳健收益才更有价值
必须结合其他指标,才能形成科学投资策略
通过合理应用夏普比率,投资者可以优化投资组合,实现稳健增长,同时掌握风险与收益的平衡。
Q1:为什么自己算的夏普值和网站不同?
A:可能原因:
数据周期不同
无风险利率假设不同
数据频率不同(日/周/月)
Q2:夏普值负数代表什么?
A:表示平均收益低于无风险利率,投资策略失败。
Q3:夏普值越高越好吗?
A:大致上是,但需确认数据周期足够长(包含牛熊市),高夏普比率可能隐藏“肥尾风险”或流动性问题。
【EBC平台风险提示及免责条款】:本材料仅供一般参考使用,无意作为(也不应被视为)值得信赖的财务、投资或其他建议。