取引
EBCについて
公開日: 2025-12-04
更新日: 2025-12-05
トレーダーの多くは、ケリー基準について聞いたことがあるでしょう。特定の投資における最適な資金配分を分析する際に、ケリー基準がまず頭に浮かぶことが多いでしょう。
1956年にベル研究所の科学者ジョン・ケリーによって初めて開発されたこの公式は、資産の期待対数成長率(幾何成長率)を最大化するために、与えられた資金に対する最適な賭け比率を計算します。
ケリー基準はギャンブル業界や金融業界で頻繁に言及されていますが、その理解は限られている場合が多くあります。この公式の理解不足や誤用は、投資家に多大な経済的損失をもたらす可能性があります。本記事では、ケリー基準について詳しく説明します。

日々の投資や取引において、私たちはしばしば2つの根本的な疑問に直面します。
期待収益がプラスの投資機会を見つけるにはどうすればよいでしょうか?
投資額/保有額をどのように決定すればよいでしょうか?
多くのプロトレーダーは、後者の疑問の方が難しいと考えています。例えば、ブラックジャックのプレイヤーは1ハンドあたりの賭け率を、不動産投資家はポートフォリオにおける不動産への配分額を、デリバティブ取引のトレーダーは新しい戦略においてどの程度のレバレッジをかけるかを決定します。
ほとんどの投資家にとって、投資機会を見つけることは、ポジションサイジングやリスク管理よりも比較的容易です。
比較的平凡な戦略でも、優れたリスク管理モデルがあれば大きな成功を収めることができると言われています。逆に、優れた戦略でも、リスク管理モデルが平凡であれば失敗する可能性があります。これは、投資と取引において、健全なポジションサイジング/リスク管理モデルが重要であることを示しています。
簡単な例
ケリー基準は、勝率と勝敗の確率が分かっており、期待収益がプラスである投資シナリオでよく用いられます。しかし、投資の期待収益がマイナスの場合、ケリーのアドバイスは賭けをしないことです。
例えば、ブラックジャックをプレイするカードカウンターは、現在の「ランカウント」と「トゥルーカウント」を知っています。つまり、次のハンドの勝敗の確率は52%対48%です。52%の勝率は確かに魅力的ですが、ギャンブラーはむしろ、次のハンドにどれだけの資金を賭けるべきかを知りたいのです。
彼は「より大きな利益を得るために賭け金を増やす」という力と、「損失と破産のリスクを減らすために賭け金を減らす」という力の間でバランスを取らなければなりません。
ケリー基準は、これら2つの力の間に最適な純資産の賭け比率が存在し、それによって長期的な富を最大化できることを示しています。
様々な賭け金の額で実証実験を行うことで、純資産が時間の経過とともにどのように変化するかを観察することができます。ギャンブラーが1ハンドごとに純資産の1%を賭けると仮定しましょう。以下は、シミュレーションで1000ハンドをプレイした場合の純資産の変化を示すグラフです。
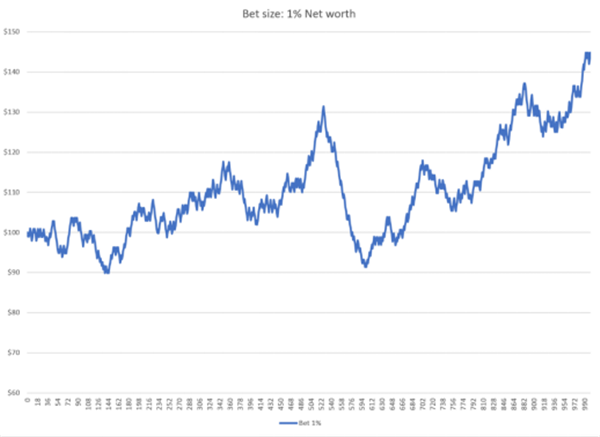
ご覧の通り、毎回1%を賭けるこの戦略は、長期的には良好なリターンをもたらしますが、ある程度の変動も見られます。1.000ハンド後、ギャンブラーの資産は44%増加しました。
もしギャンブラーが投資額のより大きな割合(つまり、純資産の割合)を各ベットに賭けていたらどうなるでしょうか?次のグラフは、1ハンドあたり純資産の1%、2%、4%を賭けた場合の純資産の長期的な変化を示しています。
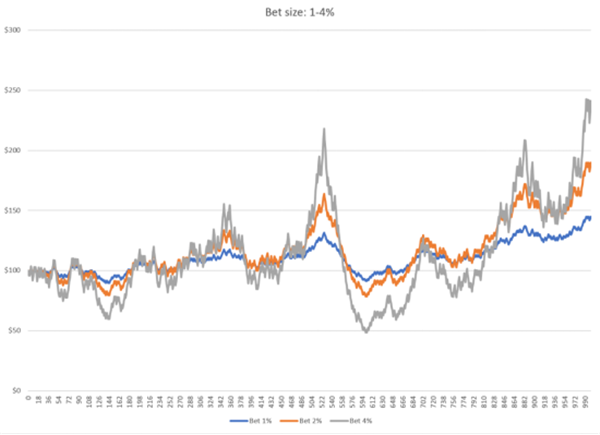
賭け金が増加すると、利益と純資産のボラティリティも同じ方向に増加することは明らかです。
私たちはさらに大きな賭け金でテストを続けています。
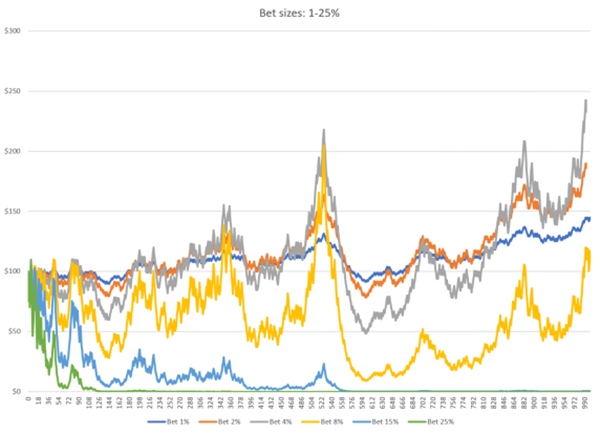
予想外のシミュレーション結果がいくつか出てきました。
賭け金の割合が1%から4%に増加するにつれて、累積利益は着実に増加しましたが、賭け金の割合が8%になると、リターンは大幅に低下しました。賭け金の割合が15%と25%になると、ギャンブラーの最終的な純資産はゼロになり、資金をすべて失うことさえありました。
賭け金の割合が増加すると、純資産の変動率は上昇し続けますが、収益性はピークに達してから反転するという結論に達しました。したがって、盲目的に大きな割合を賭けることは、資産に悪影響を及ぼす可能性があります。
このシミュレーション結果から、さらなる疑問が生じます。なぜ、利益を得られる機会があるにもかかわらず、投資を増やすと、長期的な結果が悪化するのでしょうか?
数学的検証
新しい例を用いて、このことを検証してみましょう。勝敗の確率が50/50(つまり勝率50%)、利益が6%、損失が5%の新しい投資プロジェクトです。賭け金は、全額損失の可能性まで、自由に増減(つまりレバレッジを活用)できます。
前回は、長期的な資産形成の例として、1000回の連続賭けを取り上げました。今回は、この例を単純化し、1回は勝ち、もう1回は負ける2回の連続賭けにしてみましょう。これは、長期的には勝敗比が平均50/50に近づくためです。さらに、投資の複利成長を見ているため、結果の順序は重要ではありません。したがって、反対の結果になる2つの賭けを検討することで、投資の幾何級数的成長率を合理的に推定できます。
以下は、1 回の勝ち賭け (+6%) と 1 回の負け賭け (-5%) を経験した後、初期資本 100 ドルでさまざまな賭け比率 (レバレッジ) を使用した場合の利益シナリオです。
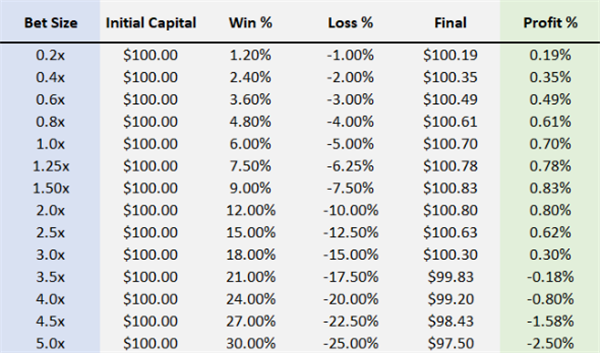
ご覧のとおり、少額投資では、レバレッジの増加に伴って利益はほぼ1対1で増加します。しかし、レバレッジが増加するにつれて利益は減少し、最終的にはマイナスになります。2倍のレバレッジの利益は1.5倍のレバレッジの利益よりも低くなります。3倍を超えるレバレッジは、実際には負け戦略です。
ここで、NGD(Negative Geometric Drag)という新しい概念が生まれます。これは、X%の利益を得た後にX%の損失(または最初に損失を得てから利益を得る)が続くことで生じる純損失を表します。例えば、ある投資で10%の損失を得てから10%の利益を得た場合(投資額 × 0.90 × 1.10)、初期投資額は1%減少します。最初に20%の損失を得てから20%の利益を得た場合、初期投資額は4%減少します。
以下は、勝率が50%で、利益と損失が等しい投資です。異なる賭け比率(つまりレバレッジ)でNGDがどのように変化するかを見てみましょう。
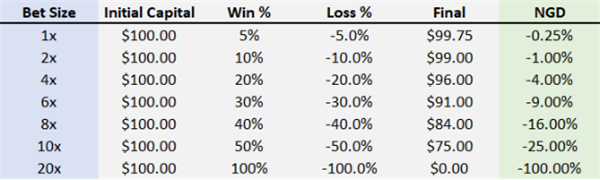
ご覧のとおり、NGDの成長率はレバレッジ比率の成長率の2乗です。
これで、レバレッジが利益にどのように影響するかをより深く理解できます。
レバレッジが増加すると、純資産増加による限界利益はレバレッジの増加に比例して増加します。しかし、複数の賭けを行うシナリオでは、NGDはレバレッジの増加に伴って横ばいに増加します。
レバレッジレベルが低い場合、限界利益が支配的な力となり、NGDは無視できるほど小さいです。しかし、レバレッジ比率が増加すると、NGDは大きくなり、最終的には限界利益を圧倒します。
次に、勝率50%、リターン6%、損失5%の投資プロジェクトに戻り、異なるレバレッジレベルにおける限界利益、NGD、最終利益の変化を見てみましょう。
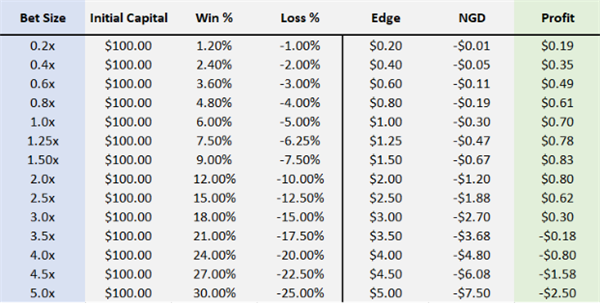
限界利益 + NGD = 最終利益
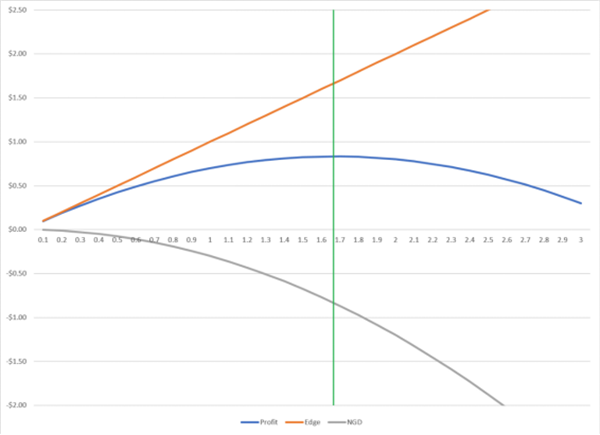
上の図に示すように、緑の縦線は限界利益とNGDの二つの相反する力が完全に打ち消し合う点(限界利益 = NGD)を表しています。これが最大利益(レバレッジ1.66倍)となる点です。これ以上のレバレッジをかけると、利益は減少します。
つまり、このレベルのレバレッジを使用することで、複数の賭け、投資、または取引における資産の幾何級数的成長率を最大化できます。
例えば、ブラックジャックでこの実験を1000回行うと、1.66倍のレバレッジでは100ドルが約6340ドルになります。3倍のレバレッジでは447ドルしか戻ってきませんが、無謀な4倍のレバレッジでは元の100ドルが2ドル未満にまで減ってしまいます。
ケリー基準
レバレッジのプラス面とマイナス面について説明したので、次はケリー基準について説明しましょう。
ケリー基準は、勝利の確率と予想される損益を考慮して、資産増加率を最大化するために各賭けに投資できる純資産の割合を計算することを目的としています。
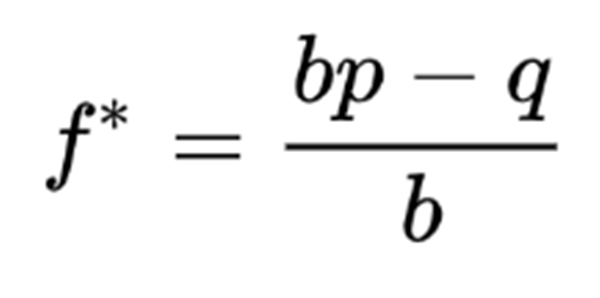
上記の式の左側にあるf*は、リスクを負うべき総資産の割合です。
右側にあるpは勝つ確率、q = 1 - pは負ける確率、bはオッズ(つまり、勝ちと負けの比率)です。例えば、2ドル勝つか1ドル負けるかのどちらかの場合、オッズは2:1なので、bを2とします。
ケリー基準をこの投資例に適用すると、
p = 50%、q = 50%、b = 1.2となります。
この場合、b = 1.2と設定することで、勝った場合の報酬(6%)が負けた場合のペナルティ(-5%)の1.2倍であることを表します。これらの値を式に代入します。
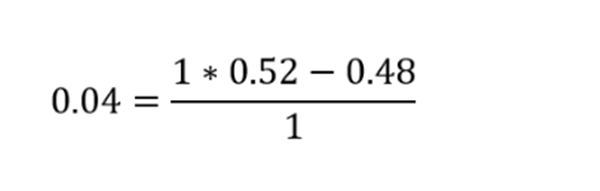
ケリー基準によれば、最適な賭け金は総資産の8.33%です。この例ではベース損失が5%なので、レバレッジは8.33%/5% = 1.66と計算されます。これは先ほど求めた値と全く同じです。
では、ブラックジャックの例を見てみましょう。プレイヤーは勝つ確率(p)が52%、負ける確率(q)が48%で、オッズは均等(b=1)です。
ケリー基準によれば、資産の4%を賭けるべきと計算されます。
上の図をもう一度見ると、ケリー基準はどちらのシナリオでも最適な賭け金を正しく計算していることがわかります。
次に、ケリー基準曲線についてさらに詳しく説明します。
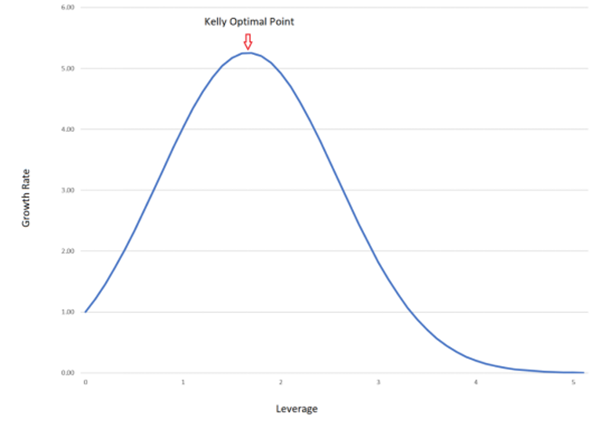
上のグラフでは、Y軸は幾何成長率、X軸はレバレッジ比率を表し、ケリーの最大値は曲線の最高点に位置しています。実際には、チャートパターンは多くの分野で類似したパターンによく似ています。
ケリー基準は主に勝率と配当(オッズ)がわかっている場合に使用され、資産成長を最大化するための適切な賭け比率を計算することができます。
ただし、ケリー基準は投資の成功確率や投資収益率の計算には使用できないことに注意することが重要です。
ケリー基準は、合理的な賭け金の範囲の限界を表しています。ケリー基準によって定められた範囲よりも1セントでも多く賭けると、リスクが増加します。つまり、分散が増加し、利益は減少します。
しかし、ほとんどの場合、賭け金がケリーの最大値に近づくにつれて、ケリー曲線の傾きは減少し、追加リスクと追加利益の比率が無限大になります。これは、投資家が期待利益をわずか1セント多く得るために、さらに10億ドルのリスクを負う可能性があることを意味します。
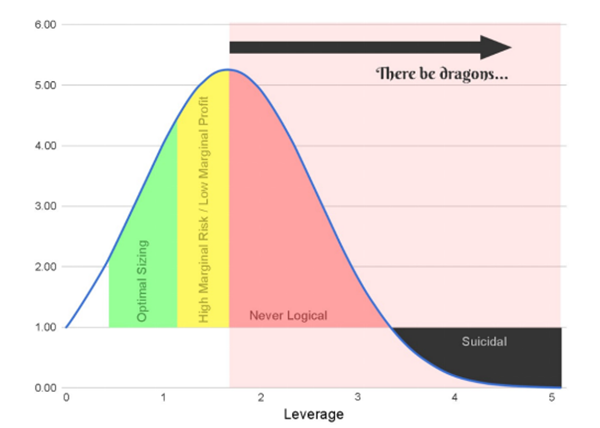
上のチャートを参照すると、緑色の領域は、特にリスク回避型の投資家にとって、比較的良好なポジションサイズを示しています。
理論 vs. 実践
理論上は、理論と実践の間に違いはありません。しかし、現実の世界では違いがあります。
ケリー基準を実際に活用するために、2つの修正が提案されています。
投資プロジェクトに関する前提を可能な限り保守的に設定してください。あらゆる状況から最悪のシナリオ(勝率、オッズ)を選択してください。ケリー基準を用いて賭け金を計算する前に、投資予測に厳密な保険をかけてください。
2ケリー基準によって計算されたポジションサイズに割引率(0.3倍や0.5倍など)を設定してください。
最初の修正は、計算式で使用される利益確率とオッズはあくまで推定値に過ぎないことを考慮しています。真の確率とリターンは隠れており、10回中9回は実際の利益は推定値よりも少なくなります。不確実な世界で投資を行う場合、保守的な前提は予想よりも現実に近くなります。これがいわゆる「安全余裕」です。
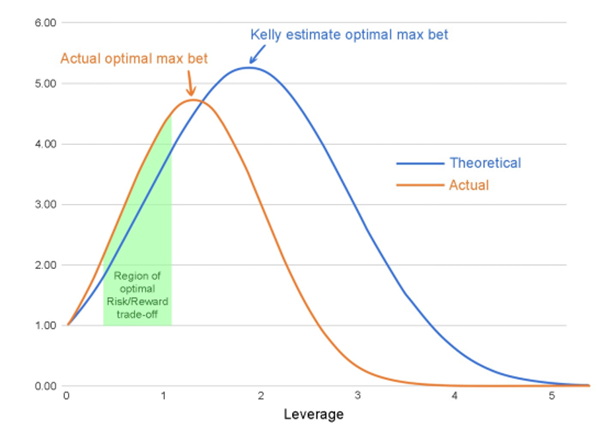
2回目の改訂は、次の観察に基づいています。
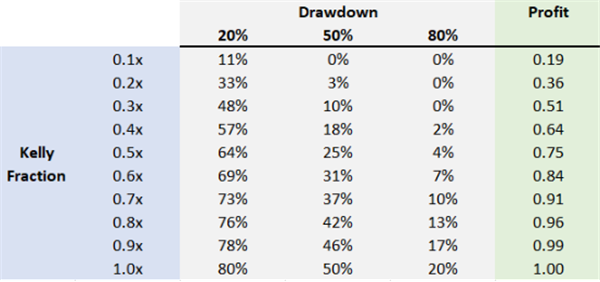
ケリー基準を用いて算出されたポジションサイズに割引係数を乗じることで、ボラティリティリスク(分散)をある程度低減できますが、それに伴う期待リターンの減少は、上記の表に示すように、分散の減少よりも小さくなります。したがって、ケリー基準の0.3倍または0.5倍のポジションサイズで賭けることで、不釣り合いに大きな期待利益を維持できます。具体的には、以下のようになります。
50%ケリー基準のポジションで賭けると、最適ケリー利益の75%を達成できますが、分散(ボラティリティリスク)は1/4しか負担しません。
30%ケリー基準のポジションで賭けると、最適ケリー利益の51%を達成できますが、分散(ボラティリティリスク)は1/9しか負担しません。
一般的な個人投資家にとって、30%ケリー基準の配分は非常に合理的で受け入れやすいものですが、プロの投資家や資産運用に携わる投資家にとって、特に下流の顧客需要が変動しやすい場合、最適なリスク管理/ポジション水準はさらに低くなります。この場合、投資取引の安定性を維持することがファンドマネージャーにとっての第一原則であり、一般的に選択される割引率はケリー基準配分の 0.1 ~ 0.15 倍です。
結論
ケリー基準は投資取引において幅広く応用されています。その中核となる原則はリスク管理であり、その基盤の上にリターンの最大化を目指しています。これは人間の合理的な取引を体現しています。最後に、ケリー基準から得られる重要なポイントをいくつか挙げます。
投資の期待収益率がプラスの場合、ケリー基準は破産することなく賭け率を上げる最速の方法を計算することができます。
投資の期待収益率がゼロまたはマイナスの場合、賭けをやめましょう。
期待収益率が同じ場合、取引システムの勝率またはオッズを上げることで、最大ポジションサイズをそれに応じて増やすことができ、資産成長率を高めることができます。
ケリー基準を様々な投資取引に適用する場合、市場状況は変化するため、ポジション計算において過度に積極的なアプローチは避けるべきです。割引率を設定することで取引リスクを軽減できます。
免責事項: この資料は一般的な情報提供のみを目的としており、信頼できる財務、投資、その他のアドバイスを意図したものではなく、またそのように見なされるべきではありません。この資料に記載されている意見は、EBCまたは著者が特定の投資、証券、取引、または投資戦略が特定の個人に適していることを推奨するものではありません。